Обобщенная кривая ростаНайдем для примера оценки параметров кривой роста, заданной четырехпараметрической формулой (11.2.3). Для этого приведем ее к линейному виду
Примем обозначение
Тогда последняя формула перепишется в виде
Рассеяние эмпирических значений случайной величины Y относительно теоретической прямой (11.3.15) будет описываться первой системой непрерывных распределений, в частности, нормальным законом. Распределение случайной величины y при заданных значениях t можно найти по распределению случайной величины Y:
Теперь можно воспользоваться формулами (11.3.3) – (11.3.5) для нахождения оценок параметров α, β, S2, заменив величины
где величина
Найдем формулы для вычисления верхней и нижней доверительных границ уровней временного ряда. На основании формулы (11.3.14) имеем
|
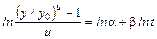. (11.3.14)
.
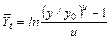. (11.3.15)
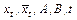соответственно на 
. Несмещенная оценка остаточной дисперсии случайной величины Yt в этом случае будет вычисляться по формуле
,
,
,
.
