Отклонения от номинального размера
детали «NN» Ø50 ±0,012
Такая форма представления данных замечательна тем, что из подобной таблицы видно, насколько тщательно были выполнены замеры контролируемого параметра. Например, в приведенной таблице резко выделяются частоты отклонений, кратных точности средства измерения (2 микрона), что свидетельствует о некорректном округлении результатов измерения. В этом случае кривая распределения находится по сгруппированным данным, причем ширина интервала принимается равной единице. Вводить следует построчно пары чисел xi, ni через запятую, а для завершения вводится 0,0. Результаты расчетов остаются прежними (кроме количества и ширины интервалов). Поскольку критерий L < 3 (В Программе он обозначен через L 1), то выравнивающее распределение относится к типу 1.1 и задается плотностью
Оценки параметров и нормирующего множителя приведены в распечатке (см. табл. 9.2.3). Случайная величина Х задана на интервале –20,71284< X <16,37711.
Таблица 9.2.3 Показатели статистического распределения (
Распределение типа 1.1 с параметрами AU = 2.696148E-02 K = 8.403986 U =.2352945 L = –20.71284 N = 1.367198E–10 Случайная величина Х задана на интервале –20.71284<X<16.37711 P(X) = N*(X–L)^(K-1)*(1-AU*(X-L))^(1/U-1)
Показатели уровня качества (
Теперь можно рассчитать любые интересующие нас показатели. Например, выбрав в меню «Вид расчета» пункт 4 (вычисление доверительных интервалов) и введя вероятность Р = 0,9973, найдем границы технологического допуска –11,0123 < X <14,4149. Для вычисления ожидаемого процента брака необходимо выбрать в меню «Вид расчета» пункт 8 (вычисление показателей уровня качества продукции). Введя затем середину поля допуска Т 0 = 0 и отклонение δ/2=12, получим ряд показателей качества (см. распечатку), в том числе прогнозируемый процент брака, равный 2,76925. Поскольку в данном случае показатель точности (коэффициент рассеяния) КТ > 1, то для полного исключения брака требуется уменьшить рассеяние. Однако только за счет смещения центров полей рассеяния и допуска можно добиться значительного уменьшения брака. Например, при вводе Т0 = 3,92, δ/2 = 12 получим процент брака 0,911558. При этом весь брак будет на нижней границе поля допуска. Следовательно, для уменьшения брака следует осуществить настройку оборудования, т.е. совместить центры полей рассеяния и допуска. Ввиду того, что в данном случае выравнивающая кривая распределения имеет небольшую левостороннюю асимметрию ( Например, при вводе Т0 = 2, δ/2 = 12 получим еще меньший процент брака, равный 0,5648. При этом он примерно одинаков на обеих границах конструкторского допуска. Для уменьшения рассеяния необходимо принимать другие меры. Эти вопросы решает отдел главного технолога завода. Сделаем некоторые выводы по рассмотренному примеру. Во-первых, выравнивающее распределение оказалось далеко не нормальным, которое характеризуется показателями Как показывает практика, нормальный закон распределения реализуется довольно редко. Если бы в данном примере в качестве выравнивающего распределения был принят нормальный закон, то ожидаемый процент брака был бы равен 4,456, т.е. в 1,6 раза больше фактического. И это при небольшой асимметрии выравнивающей кривой! В других случаях нормальный закон может давать значительно бόльшую ошибку (до 10 раз) по сравнению с фактическим браком. Отсюда следует вывод, что самым важным вопросом, который необходимо всякий раз решать при статистическом анализе точности технологического процесса – это вопрос установления наилучшей выравнивающей кривой. Он может быть решен только при использовании обобщенных распределений. Во-вторых, из рассмотренного примера видно, что разладка технологического процесса определяется двумя факторами: смещением среднего значения контролируемого параметра и рассеиванием его значений относительно среднего. В-третьих, регулирование настройки технологического процесса дает возможность уменьшить брак в 3-6 раз, хотя и не исключает его полностью, если коэффициент точности КТ > 1. В-четвертых, при наладке технологического процесса одним из основных критериев следует принимать не только величину смещения центров рассеяния и допуска, но и минимальный ожидаемый уровень брака, особенно в случае асимметричного выравнивающего распределения. С помощью Программы нетрудно подобрать оптимальное смещение центров рассеяния и допуска, при котором ожидаемый процент брака будет минимальным при заданном коэффициенте точности.
|

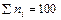
 .
.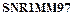 )
)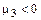 ), то необязательно точно совмещать центры полей рассеяния и допуска.
), то необязательно точно совмещать центры полей рассеяния и допуска. .
.


