Выравнивающее распределение суммы независимых случайных величин
Пусть распределение некоторой случайной величины Х задано таблицей (графы 1 – 3).
Таблица 8.2.7 Распределение случайной величины Х
Найдем по методу моментов выравнивающее распределение. По данным табл. 8.2.7 вычислим моменты случайной величины Х. Они равны: Поскольку распределение симметрично, показатель асимметрии β1=0. Показатель островершинности
Предполагая, что данное распределение описывается первой системой непрерывных распределений, по методу моментов находим, что выравнивающим является распределение I типа (бeта-распределение) с параметрами
и нормирующим множителем N = 0,107546. Распределение случайной величины Х задается плотностью
(-0,068538< x <6,068538). В табл. 8.2.7. (графа 4) приведены расчетные значения плотности р(х) при найденных оценках параметров. Они очень близки к вероятностям. Пусть далее требуется найти выравнивающее распределение суммы двух независимых случайных величин Х и Y, распределения которых заданы приведенной выше табл. 8.2.7. Эту задачу можно решить либо теоретически по правилам отыскания композиции распределений по известным плотностям слагаемых, либо эмпирически, вычислив предварительно моменты случайной величины Z=X+Y. По формулам (7.4.33) для случайной величины Z=X+Y (здесь n =2) найдем:
Далее по формулам (7.4.34) имеем:
По известным моментам распределения случайной величины Z=X+Y нетрудно рассчитать параметры и нормирующий множитель выравнивающей кривой, которая тоже относится к I типу (бeта-распределение). Они равны:
Случайная величина Z=X+Y задана на интервале –0,49182< Z <12,49182. Распределение случайной величины Z=X+Y можно задать таблично. Для этого по данным табл. 8.2.7 необходимо найти все возможные значения суммы X + Y и их вероятности, которые равны произведениям вероятностей слагаемых. В табл. 8.2.8 в первых трех графах приведено распределение случайной величины Z=X+Y при условии, что Х = Y, причем случайные величины Х и Y имеют одно и то же распределение, заданное табл. 8.2.7.
Таблица 8.2.8 Распределение суммы двух независимых одинаково распределенных случайных величин Z=X+Y
Естественно, что моменты, вычисленные по распределению случайной величины Z, совпадают с моментами, рассчитанными ранее теоретически с помощью формул (7.4.33) по моментам случайной величины Х. Кроме того, теоретические моменты выравнивающей кривой по четвертый порядок включительно совпадают с эмпирическими моментами, поскольку на этом равенстве основано вычисление выравнивающей кривой распределения. Центральные моменты более высоких порядков статистического и выравнивающего распределений могут не совпадать. Так, момент 6-го порядка случайной величины Z, рассчитанный по данным табл. 8.2.8, равен
т.е. в 1,012 раза больше эмпирического момента. Расчетные значения плотности р(z) при найденных оценках параметров приведены в табл. 8.2.8. Они близки к соответствующим вероятностям. Таким же путем может быть найдено распределение суммы независимых случайных величин, имеющих различные типы распределений, например, гамма и бeта-распределения.
|

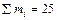

 .
. .
.


 .
. .
.

 , в то время как теоретический момент 6-го порядка равен (см. формулу (7.3.9) при r = 5, γ = k, γ u = 1)
, в то время как теоретический момент 6-го порядка равен (см. формулу (7.3.9) при r = 5, γ = k, γ u = 1) ,
,


