Выравнивание по универсальному методу моментовВ табл. 8.2.1б приведена группировка колхозов и совхозов Республики Беларусь по урожайности картофеля в 1992 г. (по данным Госкомстата Республики Беларусь). Пример 1. Рассмотрим статистическое распределение хозяйств Гродненской области по урожайности картофеля в 1992 г. (см. табл. 8.2.4, графы 1 – 3). Табл. 8.2.4 Распределение колхозов и совхозов Гродненской области
Требуется: используя универсальный метод моментов, найти выравнивающее распределение, оценить его параметры, рассчитать значения плотности в серединах каждого интервала, оценить по критерию «х u-квадрат» степень близости выравнивающей кривой к статистическому распределению. Решение. Пусть выравнивающее распределение относится к первой системе непрерывных распределений. В этом случае установление типа выравнивающей кривой осуществляется так же, как и по классическому методу моментов, т.е. вычисляются среднее, центральные моменты (2 – 4)-го порядков, показатели По статистическим данным табл. 8.2.4 находим:
С помощью номограммы (Приложение 2) устанавливаем, что выравнивающее распределение относится ко II¢ типу, поскольку Оценку параметра k можно найти по той же номограмме. В первом приближении имеем:
Они были вычислены по формулам (7.4.11):
где
Для вычисления величин Выравнивающее распределение задается плотностью
В табл. 8.2.4. в графе 4 приведены расчетные значения плотности распределения в серединах интервалов р(хi), а в графе 5 – теоретические частоты mi. Критерий согласия К. Пирсона оказался равным: χ;2 = 1,623. По таблице χ;2 – распределения при числе степеней свободы Результаты расчетов представлены на рис. 8.2.2.
Рис. 8.2.2. Распределение колхозов и совхозов Гродненской области по урожайности картофеля в 1992 г.
На рисунке указаны нижняя и верхняя границы 90%-го интервала урожайности: хн = 68,79; хв = 185,51. Это значит, что 90% хозяйств имели урожайность картофеля на интервале хн<х<xв при средней урожайности Пример 2. Табл. 8.2.5 Интервальный ряд распределения предела прочности на сжатие портландцементного раствора 28-дневного возраста [8, c.269]
Требуется: используя универсальный метод моментов, по статистическим данным табл. 8.2.5 (графы 1-3) найти выравнивающее распределение, оценить его параметры, рассчитать значения плотности в серединах каждого интервала, оценить по критерию «хu-квадрат» степень близости выравнивающей кривой к эмпирическому распределению. Вычислить нижнюю и верхнюю границы доверительного интервала при доверительной вероятности Р = 0,9545. Решение. Выравнивающее распределение задается первой системой непрерывных распределений. По программе
Выравнивающее распределение относится к III типу и имеет оценки параметров:
Параметр β вычислялся по формуле
где Произведение αu – по формуле
где
Нормирующий множитель
Выравнивающее распределение задается плотностью
В табл. 8.2.5. в графе 4 приведены расчетные значения плотности распределения в серединах интервалов, а в графе 5 – теоретические частоты mi. Критерий согласия К. Пирсона оказался равным: Верхняя и нижняя границы интервала при Р = 0,9545 равны: хн =248,7699; хв= 390,2907. При этом ширина интервала равна 141,5207 кг/см2 и составляет 4,03342 средних квадратических отклонений. Функция распределения F (хн)=0,02275; F (xв)=0,97725.
|
60,746
82,103
62,811
33,173
13,755
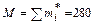
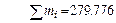
. Для расчетов используем программу 
.
, и задается обобщенной плотностью р(х).
. Более точное значение параметра k, полученное по программе, равно k = 3,10842. Оценки остальных параметров и нормирующего множителя равны: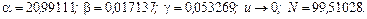
,
;
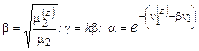(см. табл. 6.3.3).
использовались формулы (7.4.13), (7.4.14).
.
.
.
,
.
,
.
.
.
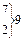
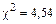
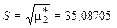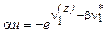, что значительно больше обычно принимаемого уровня значимости α = 0,05. Поэтому нет оснований отклонять гипотезу о согласии выравнивающего распределения III типа с эмпирическими данными.
