Первая система непрерывных распределений
Пусть распределение случайной величины Х описывается первой системой непрерывных распределений, причем тип выравнивающей кривой и оценки ее параметров заданы. Пусть далее известно, что все значения хi (i = 1,2,…, n) изменятся на постоянную величину С. Требуется найти распределение случайной величины Х + С. Рассмотрим первую плотность первой системы непрерывных распределений
Обозначим новое значение случайной величины Х через Х *, при этом Х*=Х+С. (8.3.1) Тогда распределение новой случайной величины Х * определится по формуле
Поскольку на основании (8.3.1) dх/dх * = 1, то p(х*) = p(х), (8.3.3) или с учетом плотности р (х) и (8.3.1)
Введя обозначения
последнюю плотность перепишем в виде
Таким образом, смещение случайной величины Х на постоянную С приводит к изменению параметра сдвига α и нормирующего множителя N. Параметры формы k, u не изменяются, т.е. не изменяется форма кривой распределения и, следовательно, характеризующие ее показатели (центральные моменты 2-4 порядков и др.). Поскольку случайные величины Х и Х * связаны функциональной зависимостью, причем с ростом Х растет и Х *, то их функции распределения равны F (x *) = F (x). (8.3.7) Аналогично найдем, что при увеличении случайной величины Т на постоянную С, т.е. при Т*=Т+С параметры положения (сдвига) второй и третьей плотностей первой системы непрерывных распределений будут равны
Остальные параметры и нормирующий множитель останутся без изменения. При этом вторая и третья плотности первой системы непрерывных распределений примут вид
Чтобы рассчитать новые значения плотности распределения с учетом смещения С, в случае первой системы непрерывных распределений достаточно сместить на С значения случайной величины без изменения значений плотности распределения. Если распределение случайной величины Х задано моментами Пусть
Таким образом, в случае сдвига случайной величины Х на постоянную С центральные моменты, а также среднее квадратическое отклонение, не изменятся. Изменится только среднее, что повлечет за собой изменение коэффициента вариации. По известным моментам случайной величины Х*=Х+С легко найти выравнивающее прогнозируемое распределение. Рассмотрим далее случай, когда последующие значения случайной величины Х образуются из предыдущих путем их умножения на постоянную величину С: Тогда
Показатели асимметрии и островершинности не изменятся:
По известным моментам случайной величины Х легко находятся моменты случайной величины Отметим, что в этом случае коэффициент вариации не изменится, поскольку и среднее, и среднее квадратическое отклонение увеличиваются в С раз.
|

 .
. . (8.3.2)
. (8.3.2)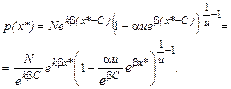 (8.3.4)
(8.3.4) , (8.3.5)
, (8.3.5) . (8.3.6)
. (8.3.6)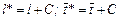 . (8.3.8)
. (8.3.8) , (8.3.9)
, (8.3.9)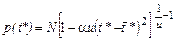 . (8.3.10)
. (8.3.10) , то ими можно воспользоваться для прогнозирования распределения.
, то ими можно воспользоваться для прогнозирования распределения.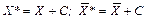 . Найдем центральные моменты
. Найдем центральные моменты 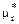 :
: .
.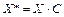 .
.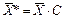 ,
, .
.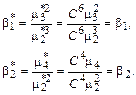
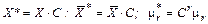 . Далее по методу моментов нетрудно найти выравнивающее распределение.
. Далее по методу моментов нетрудно найти выравнивающее распределение.


