Показатели стабильности и качества выборки
Для уверенного прогнозирования структуры выборки, которое осуществляется посредством прогнозирования выравнивающей кривой распределения, полученной в некоторый базовый момент времени, необходимо иметь оценку степени стабильности ранжированного статистического ряда распределения. Прогнозирование можно осуществлять лишь при условии неизменности порядка следования элементов в ранжированном (вариационном) ряду, т.е. при неизменности рангов элементов с течением времени. Действительно, увеличение отдельных значений хi на постоянную величину С или умножение их на ту же величину не меняет порядок их следования в вариационном ряду и, как было показано ранее, не приводит к изменению параметров формы выравнивающих кривых. Следовательно, для измерения степени связи двух ранжированных рядов распределения, а точнее, одного и того же ряда, но в разные моменты времени, может быть использован коэффициент ранговой корреляции Спирмена [14, c. 211]
где di – разность между значениями рангов одного и того же элемента выборки в двух ранжированных рядах; n – объем выборки. Коэффициент ранговой корреляции Спирмена может служить показателем степени стабильности вариационных рядов. Успешное прогнозирование структуры выборки посредством выравнивающих распределений возможно лишь при условии, когда коэффициент ранговой корреляции Спирмена близок к единице. Рассмотрим далее показатели качества выборки. Одним из таких показателей может служить величина S 1, которая в зависимости от системы непрерывных распределений задается формулами:
Чем выше показатель S 1, тем лучше качество выборки. Действительно, пусть в случае второй системы непрерывных распределений величина ti обозначает срок службы однородных изделий в i -ом интервале, либо наработку до отказа и т.д., а рi – долю изделий с данным сроком службы. Тогда качество изделий будет тем выше, чем большая их доля имеет наибольший срок службы. Вместо величины S 1 можно также использовать произведение ν;1 S 1, которое в зависимости от системы непрерывных распределений задается формулами:
Введем еще один показатель, который обозначим R(Р), например, R (P =0,9), где Р – вероятность попадания случайной величины на заданный интервал, ограниченный верхним и нижним уровнями. В зависимости от системы непрерывных распределений этот показатель задается формулами:
Вместо показателей (8.3.28), (8.3.29) могут использоваться показатели
С улучшением качества выборки показатели (8.3.27) – (8.3.31) уменьшаются. Показатель R(P) непосредственно связан еще с одним показателем качества выборки – дисперсией случайных величин
Дисперсия также уменьшается с улучшением качества выборки. С помощью приведенных показателей можно отслеживать динамику качественных изменений статистических распределений исследуемых экономических и других показателей.
|

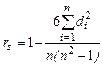 , (8.3.24)
, (8.3.24)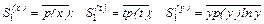 . (8.3.25)
. (8.3.25) . (8.3.26)
. (8.3.26)

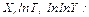
 , (8.3.32)
, (8.3.32) , (8.3.33)
, (8.3.33)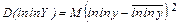 . (8.3.34)
. (8.3.34)


