Выравнивание по общему устойчивому методу
Рассмотрим примеры на выравнивание статистических распределений с помощью первой и второй систем непрерывных распределений по программам SNR1V97 и SNR2V97. Пример 1. На основании статистических данных о распределении предела прочности на растяжение портландцементного раствора 28-дневного возраста (см. табл. 8.2.3) найдем по формулам (7.5.13), справедливым для первой системы непрерывных распределений, статистические показатели
Приравнивая эти показатели соответствующим теоретическим, по номограмме (Приложение 3) устанавливаем, что выравнивающее распределение относится ко II′ типу, поскольку показатель асимметрии Теперь нетрудно вычислить оценки параметров β, γ, α и нормирующего множителя N. Используя формулы
Выравнивающее распределение задается плотностью
Если теперь рассчитать значения плотности распределения в серединах интервалов и вычислить критерий согласия К. Пирсона, то получим: Напомним, что при выравнивании по классическому методу моментов была получена вероятность Если вычислить по программе Пример 2. На основании статистических данных о распределении предела прочности на сжатие портландцементного раствора 28-дневного возраста (см. табл. 8.2.5) найдем статистические показатели
Приравнивая их теоретическим, по номограмме (Приложение 3) устанавливаем, что выравнивающее распределение относится к III типу. Поскольку показатель асимметрии В* < 0, то вначале при условии В* > 0 находим оценки параметров k′, u, затем вычисляем оценку параметра k по формуле Итак, в первом приближении из номограммы находим: Оценки параметров β, γ, произведения α u и нормирующего множителя N рассчитываются по формулам
справедливым для распределений III типа. В результате вычислений по той же программе получим:
Выравнивающее распределение задается плотностью
В данном примере критерий Нижняя и верхняя границы доверительного интервала при P = 0,9545 равны: xн = 248,2865; xв = 388,6001. Ширина интервала равна 140,3137 и составляет 3,999015 средних квадратических отклонений. Эти данные близки к результатам, полученным выше по универсальному методу моментов. Пример 3. Распределение строка службы электрических ламп [8, c.128] задано таблицей 8.2.6 (графы 2, 3). В таблице указаны значения середины интервалов при постоянной ширине интервала 200 часов. Табл. 8.2.6 Распределение срока службы электрических ламп
Пусть выравнивающее распределение задается обобщенной плотностью
которая относится ко второй системе непрерывных распределений. Для удобства расчетов разделим эмпирическую величину t на 100. От этого значения параметров k, u, β не изменятся. Не изменятся также показатели По данным табл. 8.2.6 с учетом последних замечаний вычислим статистические показатели по формулам (7.5.15):
Приравнивая эмпирические показатели
Оценки параметров вычислялись по формулам (7.5.3), (7.5.4). Нормирующий множитель N в случае распределений III типа равен (см. табл. 6.3.3)
Выравнивающее распределение задается плотностью
Критерий согласия К. Пирсона
|


 .
. . Первое приближение параметра
. Первое приближение параметра  (по номограмме). Программа
(по номограмме). Программа  V97 дает: k = 18,078269.
V97 дает: k = 18,078269. , справедливые для распределений II′ типа, найдем:
, справедливые для распределений II′ типа, найдем: .
. .
. . При числе степеней свободы r =10–3–1=6 это соответствует вероятности
. При числе степеней свободы r =10–3–1=6 это соответствует вероятности  , т.е. нет оснований отвергать гипотезу о согласии выравнивающего распределения со статистическим.
, т.е. нет оснований отвергать гипотезу о согласии выравнивающего распределения со статистическим. , при этом выравнивающее распределение относилось к типу I с параметром β=1.
, при этом выравнивающее распределение относилось к типу I с параметром β=1. нижнюю и верхнюю границы доверительного интервала при Р = 0,9545, то получим: хн =17,15092; хв = 25,05979. Ширина доверительного интервала равна 7,908873 и составляет 4,071323 средних квадратических отклонений. Эти данные близки к результатам, полученным ранее по классическому методу моментов.
нижнюю и верхнюю границы доверительного интервала при Р = 0,9545, то получим: хн =17,15092; хв = 25,05979. Ширина доверительного интервала равна 7,908873 и составляет 4,071323 средних квадратических отклонений. Эти данные близки к результатам, полученным ранее по классическому методу моментов.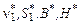 (для первой системы непрерывных распределений):
(для первой системы непрерывных распределений):
 .
. . После уточнения по методу Ньютона (по программе
. После уточнения по методу Ньютона (по программе  ) имеем: u = – 0,1301965; k ′ = 3,574764. Тогда k = 5,105934.
) имеем: u = – 0,1301965; k ′ = 3,574764. Тогда k = 5,105934.
 ,
, .
. .
. , что соответствует вероятности
, что соответствует вероятности  (при числе степеней свободы r = 11– 4 – 1 = 6).
(при числе степеней свободы r = 11– 4 – 1 = 6).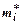

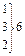

 11,89
18,74
23,26
24,06
21,56
17,27
12,68
8,71
5,71
3,61
11,89
18,74
23,26
24,06
21,56
17,27
12,68
8,71
5,71
3,61



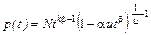 ,
, . Но значения плотности р(t) увеличатся в 100 раз (одновременно с таким же уменьшением ширины интервала).
. Но значения плотности р(t) увеличатся в 100 раз (одновременно с таким же уменьшением ширины интервала).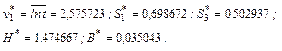
 теоретическим, по номограмме (Приложение 3) находим:
теоретическим, по номограмме (Приложение 3) находим:  . Выравнивающее распределение относится к III типу. Более точные значения параметров u, k, полученные по программе
. Выравнивающее распределение относится к III типу. Более точные значения параметров u, k, полученные по программе  , равны: u =–0,192453; k =1,584402. Оценки остальных параметров и нормирующего множителя равны:
, равны: u =–0,192453; k =1,584402. Оценки остальных параметров и нормирующего множителя равны: .
. .
. .
. , что соответствует вероятности
, что соответствует вероятности  . Это значит, что выравнивающее и статистическое распределения находятся в хорошем согласии.
. Это значит, что выравнивающее и статистическое распределения находятся в хорошем согласии.


