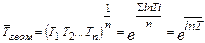Законы распределения среднего выборочного
Рассмотрим n случайных величин, распределенных по одному и тому же закону, заданному, например, обобщенной плотностью р(х) (или p(t), или р(у)). Найдем закон распределения среднего выборочного Для решения этой задачи достаточно найти центральные моменты (2–4)-го порядков среднего арифметического n независимых одинаково распределенных случайных величин и вычислить показатели асимметрии и островершинности. Далее по универсальному или классическому методу моментов с помощью программы легко устанавливается тип искомого распределения и вычисляются оценки его параметров. Известно, что математическое ожидание среднего арифметического n независимых случайных величин с одинаковыми средними равно среднему отдельной случайной величины
Найдем далее центральные моменты выборочного среднего. Для этого вначале докажем, что постоянный множитель можно выносить за знак центрального момента r -го порядка, возведя его в r -ю степень:
Действительно,
На основании (7.4.40) имеем:
Поскольку для n независимых одинаково распределенных случайных величин справедливо равенство (7.4.24)
то из предыдущего выражения получим
Найдем центральный момент третьего порядка выборочного среднего. На основании равенства (7.4.40) можем записать
Поскольку
Для центрального момента четвертого порядка среднего выборочного можем записать
Поскольку для суммы n независимых одинаково распределенных случайных величин справедливо равенство (7.4.32)
то из предыдущей формулы получим
Таким образом, моменты среднего арифметического n независимых одинаково распределенных случайных величин выражаются через моменты отдельной случайной величины посредством формул
Из формул (7.4.33) и (7.4.44) найдем взаимосвязь между моментами суммы и среднего арифметического n независимых одинаково распределенных случайных величин:
Из (7.4.45) следует, что показатели асимметрии Зная центральные моменты, а также показатели асимметрии и островершинности, по универсальному или классическому методу моментов нетрудно найти закон распределения среднего арифметического и, следовательно, вычислить доверительные границы для среднего выборочного при заданной доверительной вероятности и любом заданном значении n. С ростом n распределение среднего выборочного В случае второй системы - распределение среднего геометрического случайной величины Т
с ростом n приближается к логарифмически нормальному закону.
|

 , (или
, (или 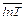 , или
, или  ) по заданному закону распределения случайной величины Х (или
) по заданному закону распределения случайной величины Х (или  , или lnlnY).
, или lnlnY). . (7.4.39)
. (7.4.39) . (7.4.40)
. (7.4.40) .
. .
.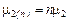 ,
,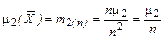 . (7.4.41)
. (7.4.41)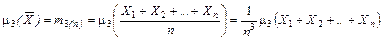 .
. (см. формулу (7.4.27)), то из предыдущего выражения получим
(см. формулу (7.4.27)), то из предыдущего выражения получим . (7.4.42)
. (7.4.42) .
. ,
,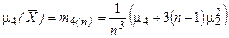 . (7.4.43)
. (7.4.43)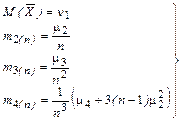 (7.4.44)
(7.4.44) (7.4.45)
(7.4.45) и островершинности
и островершинности 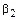 для распределений суммы и среднего арифметического n независимых одинаково распределенных случайных величин одни и те же.
для распределений суммы и среднего арифметического n независимых одинаково распределенных случайных величин одни и те же.