Центральная предельная теорема для трех систем непрерывных распределений
Используя теорию производящих функций, можно показать, что для первой системы непрерывных распределений, заданной обобщенной плотностью
моменты суммы n независимых одинаково распределенных случайных величин Производящая функция в этом случае есть
где t – вспомогательный параметр. Выразим на основании формул (7.4.33) показатели асимметрии и островершинности распределения суммы n независимых одинаково распределенных случайных величин
Из формул (7.4.34) немедленно следует центральная предельная теорема теории вероятностей (для первой системы непрерывных распределений): распределение суммы n независимых одинаково распределенных случайных величин
для которого
Формулы (7.4.33), (7.4.34) позволяют также переходить от распределения суммы n независимых одинаково распределенных случайных величин к распределению отдельной случайной величины Хi. Полученные выше результаты остаются в силе и для обобщенной плотности
т.е. в случае второй системы непрерывных распределений, если ее привести к форме плотности р (х), т.е. представить в виде
Моменты случайной величины
Формулировка центральной предельной теоремы несколько изменится: распределение суммы логарифмов n независимых одинаково распределенных случайных величин
для которого И, наконец, в случае третьей системы непрерывных распределений, заданных обобщенной плотностью
полученные выше результаты остаются справедливыми, если ее также привести к форме плотности р (х), т.е. представить в виде
Тогда моменты случайной величины
Центральная предельная теорема сформулируется в виде: распределение суммы двойных логарифмов n независимых одинаково распределенных случайных величин
для которого Здесь также оценки параметров n1(n) , α задаются формулами (7.4.36).
|

 ,
, связаны с моментами случайной величины Хi формулами (7.4.33).
связаны с моментами случайной величины Хi формулами (7.4.33).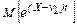 ,
, и
и  через аналогичные показатели отдельной случайной величины Хi, т.е.
через аналогичные показатели отдельной случайной величины Хi, т.е.  и
и 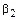 :
: (7.4.34)
(7.4.34) с ростом n приближается к нормальному закону
с ростом n приближается к нормальному закону , (7.4.35)
, (7.4.35) с ростом n перемещается по прямой от точки (
с ростом n перемещается по прямой от точки ( . (7.4.36)
. (7.4.36)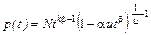 ,
,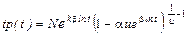 .
. будут задаваться формулами
будут задаваться формулами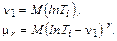
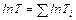 с ростом n приближается к нормальному закону, а произведение n случайных величин Т=Т 1 Т 2 …Тn – к логарифмически нормальному закону
с ростом n приближается к нормальному закону, а произведение n случайных величин Т=Т 1 Т 2 …Тn – к логарифмически нормальному закону , (7.4.37)
, (7.4.37) ,
,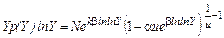 .
. будут задаваться формулами
будут задаваться формулами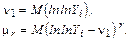
 с ростом n приближается к нормальному закону, произведение
с ростом n приближается к нормальному закону, произведение  – к логарифмически нормальному закону, а величина
– к логарифмически нормальному закону, а величина 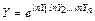 – к двойному логарифмически нормальному закону
– к двойному логарифмически нормальному закону , (7.4.38)
, (7.4.38)


