Универсальный метод моментов
За пределами применимости классического метода моментов остается широкий класс распределений, для которых не существует моментов высоких порядков. Оценки параметров таких распределений могут быть найдены по универсальному методу моментов, который впервые был описан автором в работе [10]. Основное отличие этого метода от классического метода моментов заключается прежде всего в том, что он применяется к распределениям, заданным обобщенной плотностью р(х). Другие плотности должны быть приведены к этой форме. Например, вместо плотности (6.2.8), которую представим в виде (при γ = k β)
используется плотность
Здесь последнее равенство получено из предыдущего путем умножения на t обеих его частей и использования записи Введем далее обозначение lnt = x. Тогда последнее равенство примет вид
т.е. получили обобщенную плотность р (х). Если плотность р(t) привести к форме Плотность
также приводится к форме плотности р (х). Умножим обе части последней формулы на произведение
Приняв далее обозначения Далее так же, как и в классическом методе моментов, центральные моменты Приравнивая далее эмпирические значения показателей Отметим, что статистические центральные моменты r -го порядка в зависимости от вида плотности выравнивающего распределения вычисляются по формулам: – в случае обобщенной плотности р (х)
– в случае обобщенной плотности р(t), которая приводится к форме
– в случае обобщенной плотности р(у), которая приводится к форме
где
Здесь n – число интервалов группирования статистических данных; mi – частота i-го интервала; Это обеспечивает единый порядок установления типа выравнивающего распределения и нахождения оценок параметров для трех основных систем непрерывных распределений. Эти же моменты используются для оценивания параметров трех дополнительных систем непрерывных распределений, т.е. в случае классического метода моментов. Рассмотрим для примера распределения III-V типов, заданные плотностью
Как отмечалось выше, этими распределениями можно дополнить первую (дополнительную) систему распределений (см. табл.6.5.1) при условии Выразим центральные моменты (2 – 4)-го порядков и начальный момент 1-го порядка (математическое ожидание) через параметры распределения (7.4.6). Используя теорию производящих функций, для обобщений плотности (7.4.6) получим:
где k ¢=1–1/ u – k. Показатели асимметрии β1 и островершинности β2 равны
Заменяя показатели β1, β2 их оценками, из системы двух уравнений (7.4.8) можно найти оценки двух параметров k, u, предварительно установив по тем же показателям тип выравнивающей кривой. Это – большое преимущество перед методом наибольшего правдоподобия, который требует решения четырех уравнений с четырьмя неизвестными, причем при условии, когда тип распределения заранее задан. Для нахождения оценок параметров β и α (или произведения α u) введем случайную величину Z, которая связана со случайной величиной Х зависимостью
Это уравнение является базой для построения универсального метода моментов. Найдем математическое ожидание логарифма случайной величины Z
Из последней формулы следует, что
или С учетом полученных равенств первые две формулы из четырех формул (7.4.7) можно переписать в виде
где
На основании (7.4.7¢) оценки параметра β и произведения α u равны
где n1= М(Х). При вычислении оценок β и α u центральный момент второго порядка случайной величины Х следует заменить его оценкой Аналогично выводятся формулы для оценок параметров распределений других типов, заданных плотностью р (х). Так, в случае распределений II, II¢ типов имеем
где Здесь знак "+" относится ко II типу, а "–" – ко II¢ типу. В случае распределений I, I¢ типов
где
При расчетах по универсальному методу моментов необходимо уметь вычислять с заданной точностью значения гамма-функции и ее логарифмических производных. Ниже приводятся приближенные формулы для их вычисления.
|

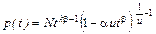 (7.4.1)
(7.4.1) , т.е.
, т.е.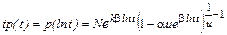 . (7.4.2)
. (7.4.2) вместо t β, что одно и то же.
вместо t β, что одно и то же.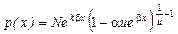 , (7.4.3)
, (7.4.3)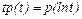 , то она будет обладать всеми свойствами плотности р(х).
, то она будет обладать всеми свойствами плотности р(х). (7.4.4)
(7.4.4) , а величину
, а величину  запишем в виде
запишем в виде  . В результате получим
. В результате получим . (7.4.5)
. (7.4.5) получим плотность (7.4.3).
получим плотность (7.4.3).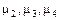 , а также показатели асимметрии
, а также показатели асимметрии  и островершинности
и островершинности  выражаются через параметры обобщенного распределения (7.4.3). При этом показатели β1 и β2 зависят лишь от двух параметров формы (k = γ/β, u) и в зависимости от их значений распределения разделяются на типы.
выражаются через параметры обобщенного распределения (7.4.3). При этом показатели β1 и β2 зависят лишь от двух параметров формы (k = γ/β, u) и в зависимости от их значений распределения разделяются на типы. теоретическим β1, β2, устанавливаем тип выравнивающей кривой распределения и находим оценки двух параметров формы k, u. Оценки двух других параметров – β, α (или произведения α u) вычисляются по простым формулам при известных оценках параметров k, u.
теоретическим β1, β2, устанавливаем тип выравнивающей кривой распределения и находим оценки двух параметров формы k, u. Оценки двух других параметров – β, α (или произведения α u) вычисляются по простым формулам при известных оценках параметров k, u. , где
, где 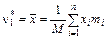 ;
;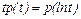 ,
, , где
, где 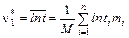 ;
;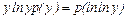 ,
, ,
,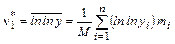 .
. - объем выборки.
- объем выборки. (7.4.6)
(7.4.6) .
.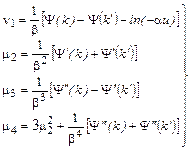 (7.4.7)
(7.4.7) (7.4.8)
(7.4.8) (см. формулу 7.4.6)) и рассмотрим ее логарифм
(см. формулу 7.4.6)) и рассмотрим ее логарифм .
. .
.
 .
. (7.4.7¢)
(7.4.7¢) - математическое ожидание случайной величины
- математическое ожидание случайной величины  ;
;  - центральный момент второго порядка случайной величины
- центральный момент второго порядка случайной величины 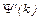 - первая производная пси-функции
- первая производная пси-функции  .
. , (7.4.9)
, (7.4.9) , (7.4.10)
, (7.4.10)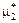 (выборочной дисперсией), а М(Х) – выборочным средним
(выборочной дисперсией), а М(Х) – выборочным средним  .
. , (7.4.11)
, (7.4.11) .
. , (7.4.12)
, (7.4.12)



