Рассмотрим далее распределения II типа.
Тип II. Критерии: u → 0; L = 3. Кривая распределения задается формулой
Покажем, что для распределений II типа величина
При u →0 формулы (7.3.11) дают
В общем случае зависимость между показателями
которая следует из (7.3.11). Подставляя значения
Далее, поскольку D*=C*–a2A *, то при А * = 0 имеем равенство D*=C * и, следовательно, D=C. С учетом полученных результатов параметры распределения (7.3.16) равны
Их можно также выразить через центральные моменты не выше 3-го порядка [9]:
В заключение отметим, что распределения II типа при Далее, поскольку для распределений II типа величина А =0, то квадратное уравнение Аа 2 +Ва+С= 0 имеет один отрицательный корень. В случае распределений I типа квадратное уравнение имеет два корня –один положительный, другой отрицательный. Для последующих расчетов необходимо принимать тот корень, знак которого противоположен знаку среднего выборочного. В случае распределений III типа квадратное уравнение имеет два отрицательных корня. Меньший из них (по абсолютной величине) соответствует распределениям III типа.
7.3.2. Распределения I¢, II¢ типов при b=1. Распределения I¢, II¢ типов заданы плотностью
которая получается из (7.3.1) при Выразим параметры распределения (7.3.20) через их центральные моменты. Представим плотность (7.3.20) в дифференциальной форме
Далее, поступая как и в предыдущем случае (см. п.7.3.1), придем к следующему уравнению
Полученное уравнение позволяет выразить в явном виде параметры распределения (7.3.20) через его центральные моменты не выше 4-го порядка. Придавая величине r значения 0,1,2,3 и учитывая, что
Из первого уравнения системы (7.3.23) находим
Далее имеем [9]
где величины А,…,Е задаются формулами (7.3.7) или (7.3.8). Выразим далее центральные моменты распределений I¢, II¢ типов, заданных плотностью (7.3.20), через параметры α, γ, u. Из (7.3.22) с учетом (7.3.24) найдем
откуда при r = 1, 2, 3 имеем
Показатели асимметрии и островершинности на основании (7.3.27) равны
Здесь также величина L входит в качестве первого сомножителя в формулу для β2, т.е.
при этом остается справедливой также формула (7.3.13). Распределения I ¢, II ¢ типов имеют моменты четвертого порядка при Исследования показали, что при |b|=1 кривая распределения I¢ типа представляет собой соответствующую кривую III типа, но смещенную вдоль оси абсцисс на величину Между параметрами распределений I¢ и III типов имеются соотношения
где штрихом отмечены параметры распределений I¢ типа. Формулы (7.3.30) позволяют осуществлять переход от распределения III типа к равносильному распределению I¢ типа. Обратный переход осуществляется по формулам
которые следуют из (7.3.30). Для обоих типов кривых корни квадратного уравнения Аа 2+ Ва + С =0 отрицательны, причем меньшему по абсолютной величине корню соответствует III тип, а большему – I ¢ тип распределения. При равных корнях имеем распределение II ¢ типа. Рассмотрим распределения II ¢ типа. Тип II¢ Критерии: u ®0, L >3. Плотность распределения задается формулой
Покажем, что для распределений II¢ типа величина D =0 и дискриминант В 2–4 АС = 0. Решая совместно три последних уравнения системы (7.3.23) с тремя неизвестными Для распределений II¢ типа параметр u ®0, следовательно,
На основании (7.3.33) можем записать
откуда имеем При D =0 параметр α распределений II¢ типа на основании (7.3.25) и (7.3.33) будет равен
Параметры распределений II¢ типа можно выразить через моменты не выше 3-го порядка. Из первых трех уравнений системы (7.3.23) при u ®0 имеем:
В заключение отметим, что распределения II ¢ типа при При u ®0 формулы (7.3.28) дают
откуда следует, что при Из формул (7.3.28) можно установить зависимость между показателями
откуда следует, что при k ® ∞ Покажем далее, что семейство кривых К. Пирсона является частным случаем системы непрерывных распределений автора, которая задана обобщенной плотностью (7.3.1) при |b|=1. Действительно, если в дифференциальное уравнение (7.3.2) вместо параметров α, γ, u подставить их значения из (7.3.6), то после преобразований будем иметь [9]
Разделив числитель и знаменатель правой части последнего уравнения на величину 2(А +3 Е), получим дифференциальное уравнение К. Пирсона
множество решений которого составляет семейство кривых распределения К.Пирсона. При этом классификация распределений осуществляется в зависимости от значений дискриминанта b 2–4 ас, откуда следует критерий К.Пирсона k=b 2 / 4 ac. В семействе кривых К. Пирсона область выше распределений II¢ типа занимают распределения IV типа по K. Пирсону, для которых 0< k <1, а дискриминант b 2–4 ac <0. Таким образом, семейство кривых К. Пирсона является частным случаем системы непрерывных распределений автора, заданной обобщенной плотностью (7.3.1) при При
где коэффициенты am, bm являются функциями параметров α, β, γ, u. При целых β величина В заключение отметим, что после нахождения оценок всех параметров распределения (7.3.1) при
где l - параметр сдвига. Он равен величине смещения начала выравнивающей кривой распределения относительно начала координат. При этом
Распределение I¢ типа запишется в виде
Поскольку здесь
|

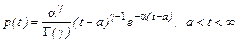 . (7.3.16)
. (7.3.16)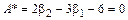 .
. (7.3.17)
(7.3.17)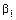 и
и  выражается формулой
выражается формулой ,
, .
.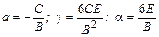 . (7.3.18)
. (7.3.18) . (7.3.19)
. (7.3.19) приближаются к нормальному закону, так как при этом условии формулы (7.3.17) дают:
приближаются к нормальному закону, так как при этом условии формулы (7.3.17) дают:  .
. , (7.3.20)
, (7.3.20) .
. . (7.3.21)
. (7.3.21)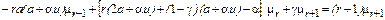 . (7.3.22)
. (7.3.22) , из (7.3.22) получим систему четырех уравнений с четырьмя неизвестными а, α, γ, u [9]:
, из (7.3.22) получим систему четырех уравнений с четырьмя неизвестными а, α, γ, u [9]: (7.3.23)
(7.3.23) . (7.3.24)
. (7.3.24) (7.3.25)
(7.3.25) , (7.3.26)
, (7.3.26)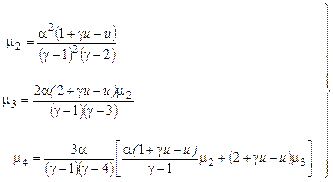 (7.3.27)
(7.3.27) (7.3.28)
(7.3.28) , (7.3.29)
, (7.3.29)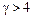 . В этом случае критерий L >3. Как было показано ранее, для распределений III типа также L >3. Но эти три типа распределений различаются с помощью параметра (критерия) u.
. В этом случае критерий L >3. Как было показано ранее, для распределений III типа также L >3. Но эти три типа распределений различаются с помощью параметра (критерия) u.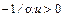 .
. , (7.3.30)
, (7.3.30)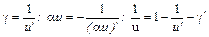 , (7.3.31)
, (7.3.31)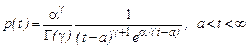 (7.3.32)
(7.3.32)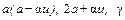 и принимая во внимание обозначения (7.3.7), получим
и принимая во внимание обозначения (7.3.7), получим  , откуда
, откуда  .
. . (7.3.33)
. (7.3.33) , (7.3.34)
, (7.3.34) , т.е. дискриминант
, т.е. дискриминант 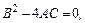 ч.т.д.
ч.т.д. . (7.3.35)
. (7.3.35) (7.3.36)
(7.3.36) (7.3.37)
(7.3.37) как в случае нормального распределения.
как в случае нормального распределения. ,
, , т.е. как и в случае распределений II типа.
, т.е. как и в случае распределений II типа. . (7.3.38)
. (7.3.38) , (7.3.39)
, (7.3.39) .
. уравнение (7.3.1) можно представить в виде
уравнение (7.3.1) можно представить в виде , (7.3.40)
, (7.3.40)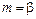 ; при нецелых β величина m = ¥.
; при нецелых β величина m = ¥. , (7.3.41)
, (7.3.41) .
.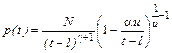 . (7.3.42)
. (7.3.42) и, следовательно, в формулах (7.3.41), (7.3.42) параметр g= k.
и, следовательно, в формулах (7.3.41), (7.3.42) параметр g= k.


