Группа симметричных распределений
Распределения функций случайного аргумента Из обобщенной плотности (6.2.8) можно получить другие распределения как функции случайного аргумент а. Если две случайные величины Х, Т связаны между собой функциональной зависимостью X=f(T), причем с ростом Х растет Т, то вероятность P(X < x) = F(x) должна быть равна вероятности P(T < t) = F(t), т.е. F(x) = F(t). (6.4.1) Найдем зависимость между плотностями распределения р(х) и р(t). По правилу дифференцирования сложной функции из (6.4.1) имеем
Воспользуемся последней формулой для нахождения других обобщенных плотностей. Пусть между двумя случайными величинами Т, Х существует взаимосвязь Т = еХ. Тогда
Характерной особенностью этой обобщенной плотности является то, что кривые III-V типов при Если
Кривые распределения, заданные тремя обобщенными плотностями p(x), p(t), p(y), имеют разнообразную форму. Например, для кривой I типа, заданной плотностью p(t), существуют формы начала и конца кривой, которые представлены ниже. Рис.6.4.1. Формы начала кривой в зависимости от значений параметра g=kb.
Рис. 6.4.2. Формы конца кривой в зависимости от значений параметра u.
|
. (6.4.2)
и, следовательно,
. (6.4.3)
являются симметричными.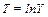
, то таким же путем получим еще одну обобщенную плотность
. (6.4.4)
