Построение системы непрерывных распределений методом обобщения
Памятка студенту Когда ты хочешь много знать, Не тратя лишних сил и времени, Старайся чаще применять Волшебный метод обобщения! Рассмотрим три простейших распределения: равномерное, треугольное убывающее и треугольное возрастающее [9, 11]. В первом случае плотность вероятности и функция распределения задаются формулами р(t)= a; F(t)= at= 1 –( 1 –at). (6.2.1) Во втором случае
В третьем случае
Обобщим попарно функции распределения (6.2.1), (6.2.2) и (6.2.1), (6.2.3) путем введения новых параметров. В первом случае получим
Во втором случае
Теперь замечаем, что в формуле (6.2.4) имеется параметр u, но его нет в формуле (6.2.5). Введем его в последнюю формулу. В результате получим
Последняя плотность может быть еще более расширена за счет введения нового параметра формы. Параметр b в формуле (6.2.7) используется дважды в качестве показателя степени. Пусть это будут два разных параметра. Тогда вместо (6.2.7) можем записать [9]
В итоге получена обобщенная плотность распределения с четырьмя параметрами a, b, g, u. Нормирующий множитель N выражается через эти параметры из условия нормировки
Последовательность обобщения простейших распределений показана на рис. 6.2.1.
|

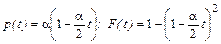 . (6.2.2)
. (6.2.2) . (6.2.3)
. (6.2.3)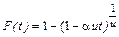 . (6.2.4)
. (6.2.4) . (6.2.5)
. (6.2.5)
 , (6.2.6)
, (6.2.6) . (6.2.7)
. (6.2.7)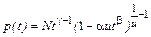 . (6.2.8)
. (6.2.8) .
.


