Статистические оценки параметров. Точность оценки, доверительная вероятность (надежность)
Выборку характеризуют такие показатели, как:
- среднее выборочное значение
- выборочная дисперсия
- центральные выборочные моменты
(все характеристики приведены для несгруппированных данных). Выборочная дисперсия является смещенной оценкой генеральной дисперсии. Несмещенной оценкой дисперсии будет исправленная выборочная дисперсия
При объеме выборки n >; 30 можно использовать неисправленную выборочную дисперсию. Среднее выборочное значение Если установить границы интервала Пусть 1– a обозначает вероятность того, что результат измерения
где 1– a - доверительная вероятность (надежность) оценки; Величина d характеризует точность оценки (в данном случае среднего) и по абсолютной величине равна
где Тогда предыдущую формулу можно переписать в виде
Величину 1–a обычно выбирают 0,9; 0,95; 0,99. Величину tna находят по таблице распределения Стьюдента в зависимости от числа степеней свободы ν = n и вероятности α.
|
(n – объем выборки);
;
.
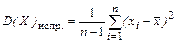является точечной оценкой математического ожидания.
, который с заданной вероятностью Р покрывает значение 
, то получим интервальную оценку.
отличается от истинного значения mx на величину, не большую d. Это записывается так:
,
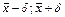– доверительный интервал.
,
– среднеквадратическое отклонение; n – объем выборки.
.
