Числовые характеристики непрерывных случайных величин
Для возможно более полного и всестороннего описания случайных величин используют различные показатели. К ним относятся: характеристики положения – математическое ожидание, мода, медиана; характеристики вариации – дисперсия, среднее квадратическое отклонение, коэффициент вариации; характеристики формы распределения – коэффициенты асимметрии и островершинности, которые выражаются через моменты. Математическое ожидание случайной величины Х задается интегралом
Свойства математического ожидания непрерывной случайной величины те же, что и дискретной случайной величины. Мода – такое значение случайной величины, при котором плотность максимальна. Медиана (Ме) случайной величины Х определяется соотношением P(X<Me)=P(X>Me). Она делит площадь под кривой распределения пополам. Дисперсия непрерывной случайной величины Х задается формулой
Коэффициент вариации
- выраженное в процентах отношение среднего квадратического отклонения случайной величины Х к ее математическому ожиданию. Центральные моменты r -го порядка (r = 2,3,4) задаются формулой
Заметим, что Коэффициент асимметрии (скошенность)
Коэффициент островершинности (эксцесс)
Примеры непрерывных распределений
|

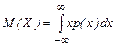 .
.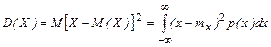 ,
,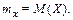
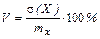
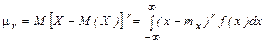 .
.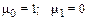 .
. или
или 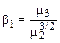 .
. или
или 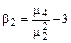 .
.


