Теорема гипотез (формула Бейеса)
Пусть имеется полная группа несовместных гипотез Н 1 ,…,Нn, при этом вероятности их равны Р(Нi). Кроме того, известны вероятности некоторого события А, которое может произойти совместно с каждой гипотезой. Пусть в результате опыта наступило событие А. Тогда распределение условных вероятностей гипотез при наступлении события А задается формулой Бейеса
Рассмотрим пример на формулу полной вероятности и формулу Бейеса, позаимствованный из [3]. Три станка выпускают одинаковые детали (см. табл.).
На складе продукция трех станков смешивается. Далее выбирается случайным образом одна деталь. Требуется: а) найти вероятность того, что она бракованная. Здесь используется формула полной вероятности. Вероятности гипотез равны (см. табл.):
Вероятности брака при каждой гипотезе равны:
Тогда
Формула полной вероятности в данном примере определяет средневзвешенную вероятность брака по трем станкам. Действительно, записав ее в более простом виде, находим
б) Найти вероятность того, что случайно отобранная деталь, оказавшаяся бракованной, выпущена первым станком. По формуле Бейеса находим
Формула Бейеса в данном примере определяет долю бракованных изделий (в общем объеме брака), изготовленных одним i -м станком.
То же для других станков
|

 .
.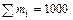

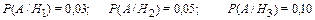 .
. .
.
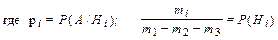 .
.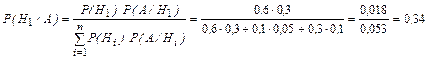 .
. .
. .
.


