Теорема сложения вероятностей (несовместных событий)
Пусть А и В – несовместные события. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий Р(А+В)=Р(А)+Р(В). Для нескольких несовместных событий имеем
Для совместных событий
где Р(АВ) – вероятность совместного появления событий А и В.
Теорема умножения вероятностей (независимых событий) Вероятность произведения (совмещения) двух независимых событий равна произведению вероятностей этих событий Р(АВ)=Р(А)Р(В). Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место Р(АВ)=Р(А)Р(В/А)=Р(В)Р(А/В). Пример. В урне 2 белых и 3 черных шара. Вынимаем подряд 2 шара. Какова вероятность того, что оба шара белые, т.е. А=А 1 А 2. Решение. А 1 – появление белого шара при 1-м испытании; А 2 – появление белого шара при 2-м испытании
Следствие теоремы умножения вероятностей. Вероятность появления хотя бы одного события из событий А 1, А 2 ,…,Аn, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
В частном случае, при
Пример. Вероятности попадания в цель каждого из трех стрелков равны: р 1=0,8; р 2=0,7; р 3=0,9. Найти вероятность хотя бы одного попадания при одном залпе. Решение. Вероятности промахов равны:
|
.
,
.
.
.
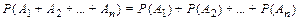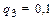. Следовательно,
.
