Свойства дисперсии
1. D(С)= 0, т.е. дисперсия постоянной величины С равна нулю. 2. D(CX)=C 2 D(X) – постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат. Доказательство:
3. D(X+Y)=D(X)+D(Y) – дисперсия суммы двух случайных величин равна сумме их дисперсий. Доказательство:
Так как M(XY)=M(X)M(Y), то последнее равенство примет вид
откуда
Приведем без доказательства еще два свойства дисперсии. 4. D(C+X)=D(X). 5. D(X–Y)=D(X)+D(Y). Отметим еще одно важное свойство дисперсии. Дисперсия числа появлений события А в n независимых испытаниях равна D(X)=npq. Доказательство: Найдем дисперсию числа появлений события А в одном испытании
Тогда Всего n испытаний, следовательно, D(X)=npq. Дисперсия имеет размерность случайность величины в квадрате. Среднее квадратическое отклонение Если извлечь из дисперсии квадратный корень, получим среднее квадратическое отклонение
Размерность величины Пример. По распределению
требуется вычислить среднее квадратическое отклонение. Решение.
Среднее квадратическое отклонение суммы взаимно независимых случайных величин равно
Доказательство. Дисперсия суммы случайных величин равна
Тогда
|
.
,
.
.
.
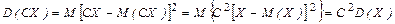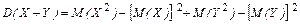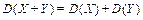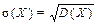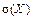та же, что и случайной величины Х.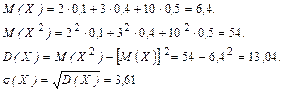
.
.
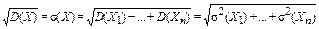