Статистическое распределение выборки. Полигон. Гистограмма. Эмпирическая функция распределения
Статистическое распределение выборки – это соотношение между значениями вариант Статистическое распределение выборки можно представить в виде таблицы, в первую строку которой записываются варианты, а во вторую – соответствующие им частоты или частости.
Здесь сумма всех частот равна объему выборки n, т.е.
а сумма частотей равна единице
Для непрерывного вариационного ряда составляется таблица, в первой строке которой указываются интервалы изменения вариант, а во второй – частоты.
Дискретные распределения можно представить полигоном, непрерывные – гистограммой. Весь вариационный ряд с размахом
Гистограмма Полигон Эмпирической функцией распределения случайной величины Х называется функция
где mx – число вариант, меньших х; n – объем выборки. Эмпирическая функция распределения является оценкой функции распределения F(x)=P(X<х).
|
и соответствующими им частотами 
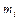или частостями (относительными частотами) 
.
,
.
разбивают на несколько интервалов 
и подсчитывают число точек (частоту) на каждом интервале. Затем на каждом интервале строится прямоугольник, площадь которого равна относительной частоте интервала. Всяплощадь гистограммы в этом случае равна единице.
,
