Метод наибольшего правдоподобия
Метод предложен английским статистиком Р. Фишером в 1912 г. Обозначим вероятность того, что в результате испытания величина Х примет значение Функцией правдоподобия дискретной случайной величины называют функцию аргумента q:
В качестве точечной оценки параметра q принимают такое его значение q*, при котором функция правдоподобия достигает максимума. Оценку q* называют оценкой наибольшего правдоподобия. Обычно вместо L используют логарифм функции правдоподобия Оценка q находится из условия Оценки метода наибольшего правдоподобия (МНП) не всегда совпадают с оценками метода моментов и часто требуют сложных вычислений. Пример. Найти для показательного закона Видоизменим несколько МНП. В качестве логарифмической функции правдоподобия используем величину Для этого вначале логарифмируем плотность р(t):
Далее находим математическое ожидание
Берем первую производную по α
Приравнивая полученное выражение нулю, находим a= 1 /М(t). Теперь осталось приравнять М(t) среднему выборочному
|
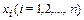, через 
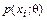(для дискретной величины).
.
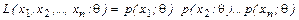, поскольку обе функции достигают максимума при одном и том же значении q.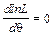
.
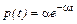оценку параметра a по МНП.
.
.
.
.
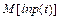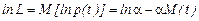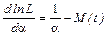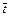и записать оценку параметра a в виде: 
.
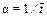