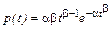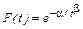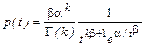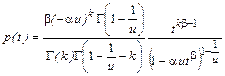Классификация обобщенных распределений
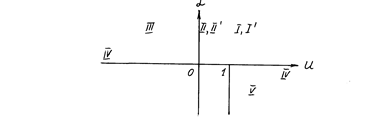
В зависимости от значений параметров a, u, а также от знака параметров b, g распределения, заданные обобщенной плотностью (6.2.8), можно разделить на типы (см. рис. 6.3.1).
Рис. 6.3.1. Классификация распределений (типы со штрихом – при b, g < 0). В таблице 6.3.1 приведены значения параметров распределений разных типов. Таблица 6.3.1 Классификация распределений
Все распределения можно разбить на две большие группы: А и Б. В группу А входят распределения с параметрами b=g, или g/b= k =1. Они задаются формулами (6.2.6) и (6.2.7). В группу Б входят распределения, заданные обобщенной плотностью (6.2.8). В этом случае функция распределения, т.е. интеграл
как правило, не выражается конечным числом элементарных функций. Отметим, что из плотности (6.2.8) при b = 2, g = 1 следует группа симметричных распределений. Симметричны также распределения I типа с параметрами b = 1, g=1/ u. Приведем все существующие типы распределений обеих групп (см. табл. 6.3.2– 6.3.4). Таблица 6.3.2 Распределения группы А
Таблица 6.3.3 Распределения группы Б
Таблица 6.3.4
|


 ,
,