Метод наибольшего правдоподобия. Покажем применение этого метода на примере распределений I типа группы Б
Покажем применение этого метода на примере распределений I типа группы Б
Примем в качестве логарифмической функции правдоподобия величину Вначале логарифмируем плотность р(t) (лучше – произведение tр(t)):
Далее находим математическое ожидание величины
Уравнения правдоподобия находятся из условий:
Приняв обозначение
Здесь последнее уравнение приведено к более простой форме с учетом первого уравнения. Оценки параметров могут быть найдены путем решения системы четырех уравнений правдоподобия – (7.2.2). При этом соответствующие математические ожидания заменяются их оценками, которые вычисляются по статистическому распределению. Однако для нахождения оценок таких величин, как Эти обстоятельства сильно ограничивают возможности использования метода наибольшего правдоподобия для нахождения оценок параметров обобщенных выравнивающих распределений.
|
.
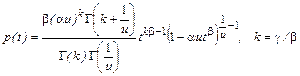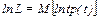[11].
(7.2.1)
.
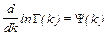для логарифмической производной гамма-функции, или иначе пси-функции, из (7.2.1) найдем
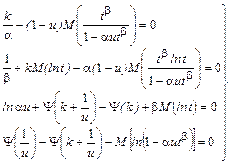(7.2.2)
и др. необходимо знать значения параметра β и произведения α u, оценки которых предстоит найти. Кроме того, предварительно необходимо знать тип выравнивающего распределения, а метод наибольшего правдоподобия не предлагает критериев для его установления.
