Классический метод моментов
Метод пригоден для оценивания параметров обобщенных распределений с параметром
7.3.1. Распределения I-III типов при β=1. Рассмотрим обобщенную плотность (6.5.2) при
Выразим параметры распределения (7.3.1) через центральные моменты. Для этого представим его в дифференциальной форме (при
Перепишем далее уравнение (7.3.2) в виде
Умножим обе части последнего равенства нa tr и проинтегрируем на бесконечном интервале (левую часть интегрируем по частям). В результате получим
Здесь первое слагаемое обращается в нуль на концах распределения, поскольку значения плотности Если начало координат перенесено в центр распределения
входящие в последнее уравнение, представляют собой центральные моменты Следовательно, последнее уравнение можно представить в виде
Учитывая, что
Из первого уравнения системы уравнений (7.3.4) получим
т.е. параметр а по абсолютной величине равен математическому ожиданию случайной величины Т. Решая далее систему уравнений (7.3.4), найдем значения параметров распределений I-III типов
где l – параметр сдвига (см. табл. 6.5.1);
Если разделить величины А,…, Е на
Величины А*,…,Е* могут использоваться в формулах (7.3.6) вместо величин А,...,Е. Выразим величины
Из (7.3.9) при r = 1,2,3 имеем [9]
Выразим с помощью формул (7.3.10) показатели
Обозначим первый сомножитель в формуле для
Величину L можно выразить через показатели
Из (7.3.13) следует, что при Таким образом, в случае симметричных распределений критерий L есть не что иное, как показатель островершинности. Из (7.3.12) следует, что критерий L в случае распределений I типа задан на интервале 1< L <3; для распределений II типа L =3, а для распределений III типа L >3. Поскольку показатель асимметрии
Из формул (7.3.10) и (7.3.12) следует, что центральный момент 4-го порядка и критерий L существуют при условии
Например, при γ=5 параметр u > – 0,125. Все остальные распределения III типа, а также распределения IV и V типов остаются за пределами применимости классического метода моментов.
|

 , т.е. в случае трех дополнительных систем непрерывных распределений, заданных плотностями (6.5.2) – (6.5.4). При этом плотности (6.5.3), (6.5.4) должны быть приведены к форме плотности (6.5.2), т.е. представлены в виде
, т.е. в случае трех дополнительных систем непрерывных распределений, заданных плотностями (6.5.2) – (6.5.4). При этом плотности (6.5.3), (6.5.4) должны быть приведены к форме плотности (6.5.2), т.е. представлены в виде .
. . (7.3.1)
. (7.3.1) . (7.3.2)
. (7.3.2)
 .
.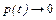 .
. , то переменная t обозначает отклонение случайной величины от ее среднего значения и поэтому интегралы вида
, то переменная t обозначает отклонение случайной величины от ее среднего значения и поэтому интегралы вида ,
, распределения (7.3.1) при
распределения (7.3.1) при  .
. . (7.3.3)
. (7.3.3) , из (7.3.3) при r = 0, 1, 2, 3 найдем
, из (7.3.3) при r = 0, 1, 2, 3 найдем


 (7.3.4)
(7.3.4)
 , (7.3.5)
, (7.3.5) (7.3.6)
(7.3.6) (7.3.7)
(7.3.7) и принять обозначения
и принять обозначения  , введенные К. Пирсоном для показателей асимметрии и островершинности, то получим:
, введенные К. Пирсоном для показателей асимметрии и островершинности, то получим: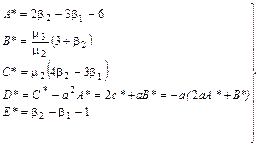 (7.3.8)
(7.3.8)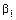 и
и  через параметры распределения (7.3.1) при
через параметры распределения (7.3.1) при  . Уравнение (7.3.3) с учетом (7.3.5) позволяет записать рекуррентную формулу для центральных моментов распределений I-III типов
. Уравнение (7.3.3) с учетом (7.3.5) позволяет записать рекуррентную формулу для центральных моментов распределений I-III типов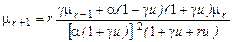 . (7.3.9)
. (7.3.9) (7.3.10)
(7.3.10) и
и  (7.3.11)
(7.3.11) . (7.3.12)
. (7.3.12) . (7.3.13)
. (7.3.13) =0 при
=0 при  , что видно из (7.3.11), то распределения I типа при условии
, что видно из (7.3.11), то распределения I типа при условии 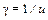 являются симметричными. Для них критерий L (обозначим его Lc) равен
являются симметричными. Для них критерий L (обозначим его Lc) равен . (7.3.14)
. (7.3.14) u > –1. А это значит, что по классическому методу моментов может быть найдена лишь незначительная часть выравнивающих распределений III типа, для которых выполняется неравенство
u > –1. А это значит, что по классическому методу моментов может быть найдена лишь незначительная часть выравнивающих распределений III типа, для которых выполняется неравенство . (7.3.15)
. (7.3.15)


