Метод наименьших квадратов
Этим методом могут быть найдены оценки параметров распределений группы А. Рассмотрим распределения I – III типов группы А. Преобразуем функцию распределения
к уравнению прямой
Построив по эмпирической функции распределения график зависимости (7.1.1) (при известной оценке параметра u) и убедившись, что опытные точки рассеиваются вдоль прямой, по методу наименьших квадратов найдем оценки величин
Тогда вместо формулы (7.1.1) запишем
Оценки параметров
Для оценки тесноты связи между переменными Y, X при различных значениях параметра u вычисляется выборочный коэффициент корреляции
В качестве оценки параметра u следует принять то его значение, при котором коэффициент корреляции максимален. Аналогично приводятся к уравнению прямой функции распределения остальных типов. Тип II: Вводя обозначения Тип II¢: Типы I¢, III¢: Из рассмотренных примеров видно, что главная трудность здесь заключается в выборе подходящего значения параметра u. Его можно найти путем подбора и вычисления при каждом значении u коэффициента корреляции. Однако имеется возможность оценить его более простым и быстрым методом. Если построить кривую распределения в форме которой произведение tp(t) максимально, равна
откуда
Последняя формула справедлива для распределений I-III типов группы А. Для распределений I¢-III¢ типов справедливо равенство
В таблице 7.1.1 приведены значения F(tc), рассчитанные по формулам (7.1.6), (7.1.7). Таблица 7.1.1 Значение функции распределения F(tc)
На основании полученных результатов можно рекомендовать следующий порядок установления типа выравнивающего распределения группы А и нахождения оценок параметров на примере плотности p(t). 1. Выбрать за начало отсчета значений случайной величины Т начало кривой распределения. 2. Найти эмпирическую моду 3. Найти эмпирическое значение функции распределения в точке C и приравнять теоретическому. 4. С помощью таблицы 7.1.1 определить два значения параметра u (в предположении, что выравнивающее распределение относится либо к I-III, либо к I¢-III¢ типам). 5. По двум значениям параметра u определить два типа возможных выравнивающих распределений. 6. Для обоих типов распределений путем построения графиков проверить, ложатся ли опытные точки на прямые. 7. В качестве выравнивающего принять наиболее подходящее распределение. Таким же образом могут быть найдены оценки параметров распределений группы А, заданных плотностями р(х), р(у). При этом плотность р(у) должна быть приведена к форме
|


 . (7.1.1)
. (7.1.1)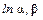 . Введем обозначения:
. Введем обозначения: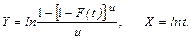
 . (7.1.2)
. (7.1.2)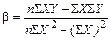 , (7.1.3)
, (7.1.3)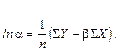 (7.1.4)
(7.1.4) (7.1.5)
(7.1.5) .
. , получим уравнение прямой (7.1.2).
, получим уравнение прямой (7.1.2). .
.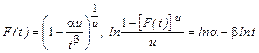 .
. и график функции распределения
и график функции распределения  , то мода
, то мода  , т.е. точка, в
, т.е. точка, в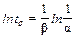 ,
, . Подставив значение tc в функцию распределения, получим [9]
. Подставив значение tc в функцию распределения, получим [9] . (7.1.6)
. (7.1.6) . (7.1.7)
. (7.1.7)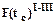
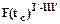
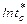 кривой распределения
кривой распределения  .
.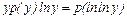 .
.


