Симметричные распределения Ic-IIIc типов
Рассмотрим симметричные распределения Ic-IIIc типов, заданные плотностью
или в дифференциальной форме
Запишем последнее уравнение в виде
Умножим обе части полученного равенства на tr и проинтегрируем на бесконечном интервале. В результате получим
При r =1 и r =3 из (7.3.44) найдем
Тогда показатель островершинности
Последняя формула совпадает с формулой (7.3.14). Величина Отсюда следует, что показатели Выразим параметры симметричных распределений Iс-IIIc типов через их центральные моменты. В случае нормального закона (тип IIc) оценка параметра α равна
Оценки параметров α, u распределений Ic, IIIc типов равны
при этом остается также справедливой общая формула
полученная ранее для распределений I-III, I¢, II¢ типов при Действительно, поскольку для симметричных распределений показатель
Тогда формула (7.3.51) в этом частном случае примет вид
что совпадает с (7.3.50). Таким образом, показатели L, u могут служить критериями для классификации как симметричных распределений с параметрами
|

 (7.3.43)
(7.3.43) .
. .
.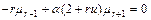 . (7.3.44)
. (7.3.44) , (7.3.45)
, (7.3.45) . (7.3.46)
. (7.3.46) будет равен
будет равен . (7.3.47)
. (7.3.47) ):
): 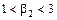 - для Ic типа;
- для Ic типа;  могут служить критериями для различения распределений Ic-IIIc типов.
могут служить критериями для различения распределений Ic-IIIc типов. . (7.3.48)
. (7.3.48)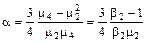 , (7.3.49)
, (7.3.49) , (7.3.50)
, (7.3.50)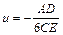 , (7.3.51)
, (7.3.51) .
. , то на основании (7.3.8) имеем:
, то на основании (7.3.8) имеем: .
. ,
, , так и других распределений I-III, I¢, II¢ типов с параметром
, так и других распределений I-III, I¢, II¢ типов с параметром  .
.


