Законы распределения суммы независимых случайных величин
Системы непрерывных распределений, заданные обобщенными плотностями, а также методы оценивания параметров, доведенные до программной реализации, позволяют более просто решать различные задачи. Пусть, например, требуется установить закон распределения суммы n независимых одинаково распределенных случайных величин Х=Х 1 +Х 2 +…+Хn. Среднее каждой случайной величины равно n1. Распределение случайной величины Хi может быть задано как аналитически, так и таблично. Поэтому для нахождения закона распределения суммы n независимых случайных величин, т.е. композиции n распределений, можно использовать общий метод. Для этого достаточно вычислить моменты суммы n независимых случайных величин n1(n), μ2(n), μ3(n), μ4(n), а также показатели β1(n) и β2(n) по известным моментам случайной величины Хi. Далее по методу моментов (универсальному или классическому) с помощью программы устанавливается тип выравнивающей кривой и находятся оценки параметров. Пусть моменты случайной величины Хi известны. Обозначим их соответственно n1, μ2, μ3, μ4. Тогда среднее суммы n независимых случайных величин будет равно
Если случайные величины Хi равны и подчиняются одному и тому же закону распределения, то
Найдем далее центральный момент второго порядка суммы n независимых одинаково распределенных случайных величин μ2(n). Начнем с рассмотрения суммы двух независимых случайных величин:
где Обозначим для краткости
Поскольку М(ху) = М(х)М(у), последнее выражение можно представить в виде
или
Но центральный момент первого порядка равен нулю. Поэтому второе слагаемое здесь равно нулю, и последняя формула примет вид
На основании рассмотренного примера можно сформулировать следующее правило: при возведении в r -ю степень суммы случайных величин х = Х–mx; y=Y–my,… в итоге следует учесть только те члены, которые не содержат первых степеней сомножителей, так как их математические ожидания равны нулю. Используя это правило, найдем центральный момент второго порядка суммы трех случайных величин
где х=Х–mx; y=Y–my; z=Z–mz. Итак,
Здесь не записаны члены, математические ожидания которых равны нулю. Следовательно,
В случае суммы n независимых одинаково распределенных случайных величин
Найдем далее выражение для центрального момента третьего порядка суммы n независимых одинаково распределенных случайных величин. Рассмотрим вначале сумму двух независимых случайных ве личин
откуда
Аналогично для суммы трех случайных величин имеем Остальные члены в квадратных скобках равны нулю. Таким образом,
Для суммы n независимых одинаково распределенных случайных величин
И, наконец, найдем выражение для центрального момента четвертого порядка суммы n независимых одинаково распределенных случайных величин. Начнем с суммы двух случайных величин
где по-прежнему
Отсюда имеем
Если Х=Y, то
Найдем далее центральный момент четвертого порядка суммы трех случайных величин
откуда
Если Х=Y=Z, то
На основании формул (7.4.29) и (7.4.31) можно записать общее выражение для центрального момента 4-го порядка суммы n независимых одинаково распределенных случайных величин.
Действительно, произведение Таким образом, моменты суммы n независимых одинаково распределенных случайных величин Х =å Хi равны
и легко вычисляются по моментам отдельной случайной величины Хi. Далее по известным моментам можно найти выравнивающее распределение суммы n независимых одинаково распределенных случайных величин. При этом найденное выравнивающее распределение может совпадать с композицией законов распределения слагаемых (например, в случае n показательных законов), но может и не совпадать с ней (например, если случайные величины распределены по закону равномерной плотности). Это связано с тем, что моменты не определяют полностью распределения.
|
. (7.4.20)
. (7.4.21)
,
.
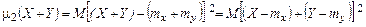. Тогда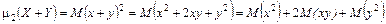
.
.
. (7.4.22)
,
.
. (7.4.23)
. (7.4.24)
,
. (7.4.25)
. (7.4.26)
. (7.4.27)
,
. Итак,
. (7.4.28)
. (7.4.29)
(7.4.30)
. (7.4.31)
. (7.4.32)
при n =2 равно 6, а при n =3 равно 18.
(7.4.33)
