В случае третьей системы - распределение среднего геометрического логарифмов отдельных случайных величин
с ростом n приближается к логарифмически нормальному закону, а величина
- к двойному логарифмически нормальному закону. При n > 100 распределение среднего выборочного Действительно, если распределение случайной величины Х (или
т.е. близкие к нормальному закону. Отметим, что формулы (7.4.34) и (7.4.44) позволяют переходить от распределения среднего арифметического n независимых одинаково распределенных случайных величин к распределению отдельной случайной величины. Полученные результаты вскрывают характер изменения показателей
которая следует из (7.4.34). При этом степень приближения к нормальному закону при больших n зависит от исходных значений показателей Установим минимально необходимое значение n, при котором распределение среднего арифметического n независимых одинаково распределенных случайных величин можно считать нормальным. Рассмотрим рис. 7.4.2. На нем точкой А ( Распределение среднего арифметического n независимых одинаково распределенных случайных величин представлено точкой В (
Заштрихованная площадь – это область нормального закона. Она ограничена двумя вертикальными и двумя наклонными отрезками прямых, тангенс угла наклона которых к горизонтальной оси принят равным 1,75. Область нормального закона может быть задана и другими способами.
Рис. 7.4.2. Фрагмент номограммы в области нормального закона Если при некотором значении n точка В (или В ¢) попадает на границу или внутрь заштрихованной области, то закон распределения среднего арифметического можно считать нормальным. Пусть точка В находится на правой вертикальной границе области нормального закона (см. рис. 7.4.2). При этом условии минимально необходимое значение n можно найти из формулы
при
Если точка В займет положение В ¢, то она будет являться точкой пересечения двух наклонных прямых, которые задаются уравнениями
Приравнивая правые части этих уравнений, найдем
Из двух полученных значений n выбираем большее. Если в формулах (7.4.48), (7.4.49) принять Рассмотрим пример. Пусть случайная величина Хi описывается распределением II¢ типа:
с параметрами: α = 12; k = 5. Тогда теоретические моменты будут равны (см. формулы (7.3.24), (7.3.27) при u →0, γ = k):
Показатели асимметрии и островершинности на основании (7.3.37) равны:
Найдем по формулам (7.4.48), (7.4.49) минимально необходимое значение n (объем выборки), при котором распределение среднего арифметического n независимых одинаково распределенных случайных величин можно считать нормальным. При
Принимаем n = 420. На практике часто ограничиваются небольшими значениями n Пусть n = 25. Тогда распределение среднего арифметического n независимых одинаково распределенных случайных величин будет иметь моменты (см. формулу 7.4.44):
Показатели асимметрии и островершинности равны:
Контроль:
Выравнивающее распределение среднего арифметического при n =25 может быть описано обобщенной плотностью
(точнее, распределением III типа первой системы непрерывных распределений) с параметрами
Зададим доверительную вероятность P = 0,9973 и найдем по одной из программ (например, Для сравнения по той же программе найдем доверительный интервал при условии справедливости нормального закона: Полученные выше формулы (7.4.48) и (7.4.49) можно использовать также для вычисления минимально необходимого значения n, при котором распределение среднего арифметического логарифмов n независимых одинаково распределенных случайных величин можно считать нормальным. Используя универсальный метод моментов, для рассмотренной выше плотности II¢ типа с параметрами
Показатели асимметрии и островершинности равны:
Далее по формулам (7.4.48) и (7.4.49) имеем (при
Принимаем n = 5. Итак, если случайная величина Х задана плотностью (7.4.50), то распределение среднего арифметического логарифма случайной величины Х близко к нормальному закону уже при n = 5, а распределение среднего арифметического самой случайной величины Х близко к нормальному закону при значительно большей величине n (n = 420). Если же центральные моменты высоких порядков не существуют (например,
|



 (или
(или 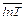 , или
, или  ) можно считать нормальным.
) можно считать нормальным. , или
, или  ) характеризуется показателями
) характеризуется показателями  (в случае трех основных систем непрерывных распределений), то распределение среднего арифметического n = 100 независимых одинаково распределенных случайных величин на основании формул (7.4.34) будет иметь показатели
(в случае трех основных систем непрерывных распределений), то распределение среднего арифметического n = 100 независимых одинаково распределенных случайных величин на основании формул (7.4.34) будет иметь показатели , (7.4.46)
, (7.4.46) с изменением числа n независимых одинаково распределенных случайных величин: с ростом n точка с координатами (
с изменением числа n независимых одинаково распределенных случайных величин: с ростом n точка с координатами ( ) приближается к точке (0; 3) по кратчайшему пути, т.е. по прямой
) приближается к точке (0; 3) по кратчайшему пути, т.е. по прямой , (7.4.47)
, (7.4.47) случайной величины Хi.
случайной величины Хi. ) обозначено распределение случайной величины Хi.
) обозначено распределение случайной величины Хi. ).
).

 :
: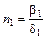 . (7.4.48)
. (7.4.48) ;
;  .
. . (7.4.49)
. (7.4.49) , то значения параметра u выравнивающих распределений по абсолютной величине будут несколько меньше 0,02 (для нормального закона u →0).
, то значения параметра u выравнивающих распределений по абсолютной величине будут несколько меньше 0,02 (для нормального закона u →0). (7.4.50)
(7.4.50)

 .
. .
.

 .
.
 и нормирующим множителем N = 3,194777E–10.
и нормирующим множителем N = 3,194777E–10. ) доверительный интервал для среднего арифметического:
) доверительный интервал для среднего арифметического: 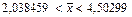 . Его ширина составляет
. Его ширина составляет  .
. . Его ширина составляет
. Его ширина составляет  , т.е. ошибка в определении границ доверительного интервала по нормальному закону оказалась существенной.
, т.е. ошибка в определении границ доверительного интервала по нормальному закону оказалась существенной. , приведенной к форме
, приведенной к форме  , найдем:
, найдем: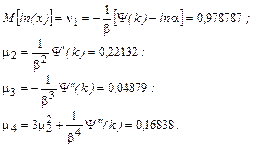
 .
. .
. ), то и величина
), то и величина  , т.е. распределение среднего арифметического случайной величины Х ни при каком n не приближается к нормальному закону.
, т.е. распределение среднего арифметического случайной величины Х ни при каком n не приближается к нормальному закону.


