Логарифм гамма-функции находится по формуле
Логарифмические производные гамма-функции на основании (7.4.13) равны:
Для облегчения различных расчетов в Приложении 1 дана таблица значений функций Точность приведенных формул тем выше, чем больше сумма х + n. Для приближенных расчетов на калькуляторе можно принять n =2, а при более точных расчетах на ПЭВМ – n =4. Рассчитаем для разных типов распределений значения показателей
Рис. 7.4.1. Классификация распределений, заданных обобщенной плотностью Как видно из рисунка, распределения II, II¢ типов представлены кривой, распределения IV типа – прямой Симметричные распределения III типа с параметрами формы В заключение отметим, что ниже прямой Для быстрого установления типа выравнивающей кривой и нахождения оценок параметров k, u по методу моментов автором построена номограмма (Приложение 2). Она строилась для распределений с левосторонней асимметрией, у которых центральный момент 3-го порядка Если статистическое распределение имеет правостороннюю асимметрию (
Аналогично для распределений I типа (β=1) при
Построенная номограмма состоит из двух частей. Верхняя часть (выше прямой Нижняя часть номограммы относится к распределениям I типа с плотностью p(t) при β=1 (т.е. типа 1.1) и является продолжением верхней части. Прямой Это дает возможность расширить основные системы непрерывных распределений за счет включения в них распределений типов 1.1 и 2.1, которые относятся к дополнительным системам непрерывных распределений (с параметром β=1). Тогда первая (основная) система непрерывных распределений SRN1 в общем случае будет включать три обобщенные плотности
Первая система непрерывных распределений включает две группы симметричных распределений: одна из них (типы IIIc-Vc) задана плотностью р(x) при k Первая система непрерывных распределений может быть также задана двумя плотностями (без последней) или даже одной плотностью р (x). Аналогично во вторую основную систему непрерывных распределений SRN2 войдут обобщенные плотности
которые получены из первой системы как распределения функций случайных аргументов: Х=lnT - для первой плотности; T=lnY – для двух других плотностей. Наконец, в третью основную систему непрерывных распределений SNR3 войдут обобщенные плотности
Вторая и третья основные системы непрерывных распределений также могут быть заданы либо двумя плотностями (без третьей), либо одной первой плотностью распределения. Для нахождения оценок параметров трех основных систем непрерывных распределений по методу моментов автором созданы программы Номограмма, представленная в Приложении 2, остается справедливой для трех основных систем непрерывных распределений.
|

 (7.4.13)
(7.4.13) (7.4.14)
(7.4.14) при
при  с шагом 0,01.
с шагом 0,01. при различных значениях параметров k, u. Далее в системе координат (
при различных значениях параметров k, u. Далее в системе координат ( ) отметим области для распределений разных типов (см. рис.7.4.1).
) отметим области для распределений разных типов (см. рис.7.4.1).
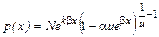 , по критериям
, по критериям 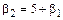 . Распределения V типа лежат ниже прямой
. Распределения V типа лежат ниже прямой  , а распределения I, I¢ типов – выше прямой
, а распределения I, I¢ типов – выше прямой 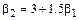
 представлены отрезком
представлены отрезком  оси ординат. С ростом параметра k распределения IIIс типа, а также II, II ¢ типов приближаются к нормальному закону, для которого
оси ординат. С ростом параметра k распределения IIIс типа, а также II, II ¢ типов приближаются к нормальному закону, для которого  .
. находится область распределений I типа, заданных плотностью (7.3.41) с параметром β=1.
находится область распределений I типа, заданных плотностью (7.3.41) с параметром β=1. .
. ), то в случае распределений III-V типов вначале с помощью номограммы находятся оценки параметров u, k¢;, затем вычисляется оценка параметра k:
), то в случае распределений III-V типов вначале с помощью номограммы находятся оценки параметров u, k¢;, затем вычисляется оценка параметра k: . (7.4.15)
. (7.4.15)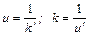 . (7.4.16)
. (7.4.16) .
.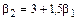 при
при  представлены распределения второго типа с параметром
представлены распределения второго типа с параметром  (гамма-распределения).
(гамма-распределения). (7.4.17)
(7.4.17) , другая (типы Ic-Vc) – плотностью р(t) при
, другая (типы Ic-Vc) – плотностью р(t) при  . Кроме того, симметричные распределения Ic типа описываются также плотностью р(t) с параметром сдвига l при ku = 1.
. Кроме того, симметричные распределения Ic типа описываются также плотностью р(t) с параметром сдвига l при ku = 1. (7.4.18)
(7.4.18) (7.4.19)
(7.4.19)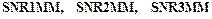 .
.


