Критерии для классификации кривых по методу моментов
Все распределения, рассмотренные в п.7.3.1 – 7.3.3, могут быть разделены на типы с помощью критериев L, u, введенных автором. Критерий L выражается через показатели асимметрии b1 и островершинности b2
При Критерий (он же параметр) u задается формулой
где величины А,…,Е или А*,…Е* вычисляются по формулам (7.3.7) или (7.3.8). На рис. 7.3.1 дана классификация распределений с параметром
Рис. 7.3.1. Классификация распределений по критериям u, L. Эти же распределения можно классифицировать по критериям
Последняя формула является следствием равенства В 2–4 АС =0, справедливого для кривых II¢ типа.
Рис. 7.3.2. Классификация распределений по критериям β1, β2. Распределения III и I¢ типов занимают одну и ту же область между распределениями II и II¢ типов, поскольку кривая I¢ типа при β=1 представляет собой соответствующую кривую III типа, но смещенную вдоль оси абсцисс на величину –1/α u >0. Распределения I типа занимают область между двумя прямыми - Эту область покрывают распределения III-V типов, принадлежащие трем основным системам непрерывных распределений. На рис. 7.3.2 последние расположены ниже прямой β2=6+0,75β1. Распределения IV типа (при Сделаем некоторые выводы. Рассмотренный выше классический метод моментов оценивания параметров имеет существенные недостатки. Во-первых, он применим лишь к распределениям, имеющим моменты вплоть до четвертого порядка, при этом параметр Как показала практика, этот метод хорошо работает в случае выравнивающих распределений I типа, заданных на ограниченном с обеих сторон интервале, особенно если распределение близко к симметричному. Для того, чтобы полнее использовать возможности обобщенных распределений по выравниванию статистических рядов распределения, необходимо иметь общие методы оценивания параметров для распределений всех типов, в том числе не имеющих моментов выше нулевого порядка (в традиционном их понимании). Методы должны быть общими для трех плотностей (6.2.8), (6.4.3), (6.4.4). Ниже рассматриваются два таких метода, разработанные автором.
|

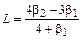 .
. (в случае симметричных распределений) показатель
(в случае симметричных распределений) показатель 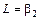 , т.е. он совпадает с показателем островершинности.
, т.е. он совпадает с показателем островершинности. ,
, , а также симметричных распределений, для которых критерий L задается формулой
, а также симметричных распределений, для которых критерий L задается формулой  .
.
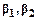 (рис.7.3.2). В этом случае распределения II типа представлены прямой
(рис.7.3.2). В этом случае распределения II типа представлены прямой  . Распределения II¢ типа – кривой
. Распределения II¢ типа – кривой .(7.3.52)
.(7.3.52)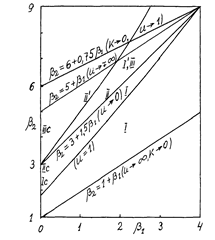
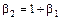 и
и 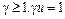 ) находятся на интервале 1,8<β2<3 оси ординат. Выше кривой II¢ типа находится область распределений, для которых дискриминант
) находятся на интервале 1,8<β2<3 оси ординат. Выше кривой II¢ типа находится область распределений, для которых дискриминант  ) лежат на прямой β2=5+β1.
) лежат на прямой β2=5+β1.


