Выравнивание по классическому методу моментов
Рассмотрим примеры на выравнивание статистических распределений обобщенными плотностями. В табл. 8.2.1 приведена группировка колхозов и совхозов Республики Беларусь по урожайности основных сельскохозяйственных культур в 1992 г. по данным Госкомстата Республики Беларусь: а) зерновые и зернобобовые культуры; б) картофель. К сожалению, группировка выполнена не совсем корректно: для анализа табличных данных желательна разбивка на интервалы равной ширины, причем не должно быть открытых интервалов, таких, как до 15ц/га, более 55 ц/га. Пример 1. Рассмотрим статистическое распределение хозяйств Минской области по урожайности зерновых и зернобобовых культур в 1992 г. (см. табл. 8.2.2, графы 1 – 3).
Табл. 8.2.1
Группировка колхозов и совхозов Республики Беларусь по урожайности основных сельскохозяйственных культур в 1992 г. а) Зерновые и зернобобовые культуры
б) Картофель
Табл. 8.2.2 Распределение колхозов и совхозов Минской области по урожайности зерновых и зернобобовых культур в 1992 г.
Требуется: используя классический метод моментов, найти выравнивающее распределение, оценить его параметры, рассчитать значения плотности в серединах каждого интервала, оценить степень близости выравнивающей кривой к статистическому распределению. Решение. Вычислим по данным табл. 8.2.2. среднюю урожайность, дисперсию, центральные моменты 3-го и 4-го порядков и некоторые другие показатели. Так как данные сгруппированы (в 9 интервалов равной ширины h =5), то моменты вычисляем по формулам
В результате найдем
Тогда среднее квадратическое отклонение S и коэффициент вариации V будут равны:
Приравнивая эмпирические моменты соответствующим теоретическим, вычислим показатели асимметрии и островершинности, а также критерий L
По рис. 7.3.1 находим, что выравнивающее распределение относится к I типу с параметром β = 1, поскольку L<;3. В этом случае оценки параметров находятся по формулам (7.3.6):
где величины А,…,Е выражены через показатели
Подставляя в последние формулы оценки показателей А =–0,343314; В =12,17618; С =546,0952; Е =1,872575. Решим далее квадратное уравнение Аа2+Ва+С =0. Корни его равны: а 1=–25,91447; а 2=61,38106. Для одного из корней должно выполняться равенство а =–n1 (хотя бы в первом приближении). Поэтому параметр а здесь равен (при а = –25,91447. Тогда D = 2C + aB = 776,6512. Теперь можно рассчитать оценки параметров по формулам (7.3.6):
Нормирующий множитель N равен
Выравнивающее распределение задается формулой (7.3.41)
где Подставляя сюда оценки параметров Все приведенные здесь расчеты выполнялись по программе SNR1MM97. Оценки параметров u, Эти оценки близки к найденным оценкам по программе. Оценим далее степень близости выравнивающей кривой к статистическому распределению по критерию «xu -квадрат» К. Пирсона:
где n – число интервалов. Умножим значения плотности на величину Объединим два последних интервала в один, что рекомендуется делать при частоте mi < 5, и вычислим для каждого интервала (всего 8 интервалов) значения величин Критерий По таблице Поскольку эта вероятность достаточно высокая, т.е. значительно больше обычно принимаемого критерия значимости α = 0,05, то нет оснований отвергать принятую гипотезу о выравнивающем распределении. Теперь можно построить гистограмму и кривую распределения. Для построения гистограммы необходимо вычислить эмпирическую плотность в каждом интервале. Она рассчитывается по формуле
где Кривая распределения строится по значениям теоретической плотности в серединах интервалов. Результаты представлены на рис. 8.2.1. На графике отмечена средняя урожайность Это значит, что 90% хозяйств имели урожайность зерновых и зернобобовых на интервале tн<t<tв. Дальнейшие расчеты показывают, что из семи статистических распределений, заданных таблицей 8.2.1а, только одно (Гродненская область) описывается обобщенной плотностью
при u <0, т.е. кривой III типа. Остальные шесть распределений описываются плотностью (7.3.41)
с параметром u > 0, т.е. кривыми I типа. Это – известные бета-распределения.
Рис. 8.2.1. Распределение колхозов и совхозов Минской области по урожайности зерновых и зернобобовых культур в 1992 г.
Кривые распределения несколько различаются как по расположению на горизонтальной оси, так и по форме. Так, кривая распределения хозяйств Брестской области по урожайности зерновых и зернобобовых культур смещена вправо относительно аналогичной кривой для Республики в целом, а кривая по Витебской области – влево. Последняя кривая отличается сильной правосторонней асимметрией. Такая форма кривой может свидетельствовать о том, что меньшая урожайность уже вряд ли возможна, а также о наличии резервов повышения урожайности либо о неблагоприятных климатических и других условиях для данной культуры. Пример 2 Табл. 8.2.3 Интервальный ряд распределения предела прочности на растяжение портландцементного раствора 28-дневного возраста [8, c.269]
Требуется: по данным табл. 8.2.3 (графы 1 – 3) найти по классическому методу моментов выравнивающее распределение, оценить его параметры, рассчитать значения плотности в серединах каждого интервала, оценить степень близости выравнивающей кривой к статистическому распределению. Найти границы доверительного интервала при заданной доверительной вероятности Р = 0,9545. Решение. Вычислим по статистическим данным с помощью программы SNR1MM97 среднее значение предела прочности, дисперсию, центральные моменты 3 и 4-го порядков и другие показатели. В результате найдем:
Среднее квадратическое отклонение S и коэффициент вариации V равны:
Приравнивая эмпирические моменты соответствующим теоретическим, вычислим показатели асимметрии и островершинности, а также критерий L
Поскольку L < 3, выравнивающее распределение относится к I типу с параметром b=1 и задается плотностью
Вычислим значения величин А,…,Е:
Решим далее квадратное уравнение Аа2+Ва+С= 0. Корни его равны: а 1 = – 6,59544; а 2 = 9,824492. Поскольку Тогда D= 2 С+аВ= 68,35499. Теперь можно рассчитать оценки параметров:
Нормирующий множитель N = 5,314906·10–4. Кривая распределения задана на интервале 14,27656<t<30,69649. Рассчитаем при найденных оценках параметров Вычислим критерий «xu -квадрат» К. Пирсона. Объединив частоты двух первых и двух последних интервалов, получим Вычислим по Программе нижнюю и верхнюю границы доверительного интервала при доверительной вероятности Р = 0.9545: tн = 17,25485; tв =24,88674. При этом значение функции распределения F(tн)= 0,02275; F(tв)= 0,97725. Ширина доверительного интервала равна 7,63189 кг/см2 и составляет 3,92874 средних квадратических отклонений.
|



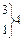
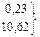 60,79
129,09
146,10
103,03
48,56
15,64
60,79
129,09
146,10
103,03
48,56
15,64


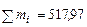

 .
. .
. .
. .
.
 и центральные моменты с помощью формул (7.3.8):
и центральные моменты с помощью формул (7.3.8):
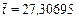 )
) .
. .
. ,
,
 и нормирующего множителя N, рассчитаем в серединах каждого интервала значения плотности вероятностей (см. табл. 8.2.2. графа 4).
и нормирующего множителя N, рассчитаем в серединах каждого интервала значения плотности вероятностей (см. табл. 8.2.2. графа 4). , можно найти по номограмме (Приложение 2). При заданных значениях
, можно найти по номограмме (Приложение 2). При заданных значениях  с учетом неравенства
с учетом неравенства  имеем: u ¢ = 0,10; k ¢ = 25. Тогда u = 1/ k ¢ = 0,04; k = 1/ u ¢ = 10.
имеем: u ¢ = 0,10; k ¢ = 25. Тогда u = 1/ k ¢ = 0,04; k = 1/ u ¢ = 10. ,
, . Получим теоретические частоты в каждом интервале (графа 5).
. Получим теоретические частоты в каждом интервале (графа 5). (графа 6). При этом теоретическая частота первого интервала (0,23) добавлена к частоте второго интервала.
(графа 6). При этом теоретическая частота первого интервала (0,23) добавлена к частоте второго интервала. оказался равным 2,615. По таблице квантилей
оказался равным 2,615. По таблице квантилей  . Оно равно 7,815. Поскольку
. Оно равно 7,815. Поскольку 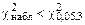 , то нет оснований для отклонения гипотезы о том, что закон распределения хозяйств Минской области по урожайности зерновых и зернобобовых культур в 1992 г. относится к распределению I типа (бета-распределению) с найденными оценками параметров.
, то нет оснований для отклонения гипотезы о том, что закон распределения хозяйств Минской области по урожайности зерновых и зернобобовых культур в 1992 г. относится к распределению I типа (бета-распределению) с найденными оценками параметров. ,
, - число хозяйств в i -ом интервале; h – ширина интервала.
- число хозяйств в i -ом интервале; h – ширина интервала. ц/га, а также нижняя tн = 16,65 и верхняя tв =39,22 90%-ные границы.
ц/га, а также нижняя tн = 16,65 и верхняя tв =39,22 90%-ные границы.





 78,37
142,17
188,10
194,49
162,08
109,66
59,52
25,06
78,37
142,17
188,10
194,49
162,08
109,66
59,52
25,06




 .
. .
. .
. .
.
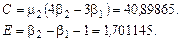
 , то параметр а здесь равен а = –6,59544.
, то параметр а здесь равен а = –6,59544.
 и нормирующего множителя N значения плотности вероятностей (см. табл. 8.2.3, графа 4). Умножив значения плотности на М·h = 1000, получим теоретические частоты в каждом интервале (графа 5).
и нормирующего множителя N значения плотности вероятностей (см. табл. 8.2.3, графа 4). Умножив значения плотности на М·h = 1000, получим теоретические частоты в каждом интервале (графа 5). . Далее по таблице
. Далее по таблице  (число интервалов после объединения стало равным 10; 4 – количество параметров обобщенного распределения) и
(число интервалов после объединения стало равным 10; 4 – количество параметров обобщенного распределения) и 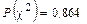 . Это значит, что нет оснований для отклонения принятой гипотезы о выравнивающем распределении.
. Это значит, что нет оснований для отклонения принятой гипотезы о выравнивающем распределении.


