На основании плотности (6.5.2) можно получить три дополнительные системы непрерывных распределений.
Первая дополнительная система непрерывных распределений в общем случае задается формулой (6.5.2) при |b| = 1, а в случае симметричных распределений – при b = 2, g = 1. Ее легко получить из второй основной системы непрерывных распределений. Для этого достаточно в табл.6.3.3 принять |b| = 1, tb заменить на Для обозначения типов кривых дополнительной системы непрерывных распределений будем использовать двузначный код, записанный арабскими цифрами через точку: 1.1, 1.1¢, 2.1 и т.д., где первая цифра обозначает тип кривой, а вторая (единица) указывает на то, что параметр b=1; единица со штрихом соответствует параметру В большинстве случаев в тексте используется единое обозначение типов, но при необходимости указывается, что |b| = 1. В таблице 6.5.1. приведены существующие типы первой дополнительной системы непрерывных распределений. Из симметричных распределений приведен один нормальный закон. Распределения типа 1.1 при k = 1 /u также являются симметричными. Первая дополнительная система непрерывных распределений представляет собой основную часть семейства кривых К. Пирсона. Таблица 6.5.1 Первая дополнительная система непрерывных распределений
Вторая дополнительная система непрерывных распределений получается из первой при t = ln y и прежних значениях параметров b, g. При этом обобщенная плотность имеет вид
Третья дополнительная система непрерывных распределений получается из второй при
|

 , а в табл. 6.3.4 заменить величину t 2 на
, а в табл. 6.3.4 заменить величину t 2 на  .
.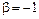 (см. табл.6.5.1).
(см. табл.6.5.1).
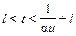




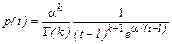
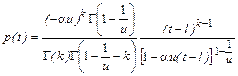



 . (6.5.3)
. (6.5.3)
 . (6.5.4)
. (6.5.4)


