Методы построения обобщенных распределений
Для получения универсальных (обобщенных) распределений используются различные методы. Наиболее известным является метод выравнивания дискретных распределений (метод К. Пирсона). Другой широко известный метод – получение нового распределения как функции случайного аргумента с известным распределением. В настоящем пособии и в других работах автора широко используется метод обобщения. Он позволяет подчас простыми и доступными средствами получать новое знание. Но для этого необходимо использовать различные его возможности. В одних случаях для получения более общих зависимостей достаточно воспользоваться одним из предлагаемых ниже приемов или их комбинацией: - введение новых параметров, объединяющих частные случаи в единое целое; - использование подходящего замечательного предела; - замена переменной; - разложение функции в степенной ряд; - получение новой более точной математической модели из двух менее точных и т.д. В других более сложных случаях требуется введение новых понятий. Но здесь не существует готовых рецептов и успех зависит исключительно от изобретательности исследователя. В результате обобщения должна получиться математическая модель, включающая как частные случаи исходные функции. Метод обобщения, несмотря на свою чрезвычайную простоту, позволяет строить универсальные математические модели, включающие как частные случаи наперед заданные зависимости, которые на практике реализуются чаще других. Что касается обобщенных распределений, то они должны включать как частные случаи подавляющее большинство известных из теории вероятностей и математической статистики распределений, ибо только в этом случае будет достаточно высока вероятность нахождения такой выравнивающей кривой распределения, которая наилучшим образом описывает статистический ряд распределения. Приведем примеры. Произведение ряда натуральных чисел Если построить график зависимости n!=f(n), то получим ряд точек. Для осуществления различных расчетов необходимо иметь непрерывную кривую, проходящую через эти точки. Непрерывным аналогом и обобщением этой зависимости, включающей при целых n значения n!, является гамма-функция, введенная Л. Эйлером
При целых n
Гамма-функция обладает свойством
При Рассмотрим другой пример, в котором для получения более общей зависимости используется замечательный предел и вводятся новые параметры. Пусть требуется найти некоторое обобщенное уравнение, включающее как частные случаи уравнения прямой и экспоненты:
Используя замечательный предел
можем записать искомое уравнение в общем виде
где b, u – новые параметры. При u = 1, b = 1 имеем уравнение прямой, а при u ®0, b = 1 – уравнение экспоненты. Полученное четырехпараметрическое уравнение имеет более широкие возможности по выравниванию и прогнозированию различных статистических зависимостей, поскольку оно включает как частные случаи кроме двух исходных множество других функций. Более того, на его основе можно получать новые уравнения, например, путем замены независимой переменной х на Рассмотрим еще примеры, в которых на базе двух приближенных равенств получается новое, более точное равенство. Пусть имеется простейшая степенная функция
где параметр a близок к нулю. Найдем формулы для вычисления логарифма х и числа х по его логарифму. Представим функцию
и разложим ее в степенной ряд
Оставив в полученном ряде два первых члена, при малых a имеем приближенные равенства
которые получаются при a>0 и a<0. Найдем среднее геометрическое величины х при α→0:
Таким же образом можно получить среднее геометрическое величины
Последняя формула позволяет весьма точно вычислять логарифмы чисел (например, от 1 до 1000 при a = 0,0001). Аналогично можно получить приближенную формулу для вычисления функции ех. Известно, что
При a®0 можем записать
откуда нетрудно получить следующую формулу
При х = 1, a = 0,0001 эта формула дает оценку е = 2,71828181, т.е. с точностью до 7 верных цифр после запятой, в то время как по известному замечательному пределу при том же a имеем только три верных цифры после запятой
|

 обозначается n! (читается «эн-факториал»).
обозначается n! (читается «эн-факториал»). .
.
 .
. . При n = 1 и n = 2 гамма-функция равна единице, поскольку 0!=1; 1!=1.
. При n = 1 и n = 2 гамма-функция равна единице, поскольку 0!=1; 1!=1. .
. ,
, ,
, и т.д.
и т.д. ,
, в виде
в виде
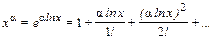

 .
. :
: .
.

 .
. .
.


