Одинаково распределенные взаимно независимые случайные величиныРассмотрим n взаимно независимых одинаково распределенных случайных величин Х 1 ,Х 2 ,…,Хn. Для них среднее арифметическое равно
Докажем три положения [3]: 1. Математическое ожидание среднего арифметического n взаимно независимых одинаково распределенных случайных величин равно математическому ожиданию а каждой из величин
Доказательство:
2. Дисперсия среднего арифметического n взаимно независимых одинаково распределенных случайных величин в n раз меньше дисперсии D каждой из величин:
Доказательство: Так как постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат, то
3. Моменты (начальные, центральные) дискретной случайной величины Начальный момент порядка r – это математическое ожидание случайной величины Хr
Например, начальные моменты первого и второго порядков равны ν;1 =M(X); ν 2 =M(X 2 ). Центральный момент порядка r задается формулой
при этом Центральный момент второго порядка представляет собой дисперсию. Между начальными и центральными моментами существуют соотношения
Следовательно, формула для вычисления дисперсии может быть записана в виде
|
.
.
.
.
.
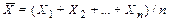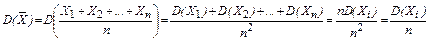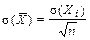(следует из п.2), т.е. среднее арифметическое n взаимно независимых одинаково распределенных случайных величин имеет значительно меньшее рассеяние (в 
раз), чем каждая отдельная величина.
.
,
.
.
