Ориентирование по осевому меридиану зоны
Дирекционным углом линии называется угол, отсчитанный по ходу часовой стрелки от северного направления осевого меридиана зоны до направления линии; он обозначается буквой α; (рис.1.14). Пределы изменения дирекционного угла от 0o до 360o.
Рис.1.14
Рис.1.15 Поскольку направление осевого меридиана для зоны одно, то дирекционный угол прямой линии одинаков в разных ее точках, а обратный дирекционный угол прямой линии отличается от прямого ровно на 180o:
Связь географического азимута и дирекционного угла одной и той же прямой линии выражается формулой:
где γГ - гауссово сближение меридианов в точке начала линии. Передача дирекционного угла на последующую сторону через угол поворота. Пусть имеются две линии BC и CD; угол поворота между ними в точке C равен β л (левый угол поворота) или β пр (правый угол поворота) - рис.1.15. Проведем через точки B и C направления, параллельные осевому меридиану зоны и покажем на рисунке дирекционные углы αBC и αCD. В задаче известны αBC и βл (или βпр); требуется найти αCD. Продолжим линию BC и покажем на ее продолжении угол αBC. Из рис.1.15 видно, что αCD = αBC + x. Но x = βл- 180o или x = 180o - βпр, тогда:
или Если при вычислении по двум последним формулам дирекционный угол получается отрицательным, к нему прибавляют 360o; если он получается больше 360o, то из него вычитают 360o.
Рис.1.13 Проведем на поверхности сферы экватор и параллель точек A и B; в плоскости параллели проведем радиусы параллели FA = r и FB = r; угол между ними равен разности долгот точек. Через точки A и B проведем полуденные линии AN и BN, которые, пересекаясь на продолжении оси вращения Земли, образуют угол γ, являющийся сближением меридианов точек A и B. Требуется выразить Рис.1.13 угол γ через координаты точек A и B, то есть, через широту φ и долготы λA и λB, причем Δλ = λB - λA. Выразим длину дуги AB двумя способами: из ΔABN BN*γ=r* Δλ, (1.11) откуда Радиус параллели выразим из Δ OFB r = R*Cos(φ), а отрезок BN - из ΔONB BN = R * Ctg(φ), где R - радиус сферы; тогда γ = Δ λ * Sin(φ) или
В этой формуле размерность γ соответствует размерности λ. Гауссово сближение меридианов. Частным случаем сближения меридианов является гауссово сближение меридианов, когда начальная точка A лежит на осевом меридиане зоны. Величина гауссова сближения меридианов, равного сближению меридиана точки и осевого меридиана зоны, является одной из характеристик положения точки внутри зоны. Формула гауссова сближения меридианов имеет вид
Буквами L и B здесь обозначены геодезические долгота и широта точки, буквой L0 - долгота осевого меридиана зоны. В пределах зоны гауссово сближение меридианов не может превышать величины 3o*Sin(B).
|



 (1.15)
(1.15) (1.16)
(1.16) , (1.17)
, (1.17) . (1.18)
. (1.18)
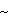 AB = BN * γ и из ΔABF
AB = BN * γ и из ΔABF  . (1.12)
. (1.12) (1.13)
(1.13) (1.14)
(1.14)


