Количество информации. В вычислительнойтехнике в качестве единицы информации условились принять один бит (англ
В вычислительнойтехнике в качестве единицы информации условились принять один бит (англ. bit – bi nary, digi t – двоичная цифра). Бит в теории информации – количество информации, необходимое для различения двух равновероятных сообщений. А в вычислительной технике битом называют наименьшую «порцию» памяти, необходимую для хранения одного из двух знаков «0» и «1», используемых для внутримашинного представления данных и команд. Бит – слишком мелкая единица измерения. На практике чаще применяется более крупная единица – байт, равная восьми битам. Широко используются также ещё более крупные производные единицы информации: – 1 Килобайт (Кбайт) = 1024 байт = 210 байт, – 1 Мегабайт (Мбайт) = 1024 Кбайт = 220 байт, – 1 Гигабайт (Гбайт) = 1024 Мбайт = 230 байт. В последнее время в связи с увеличением объёмов обрабатываемой информации входят в употребление такие производные единицы, как: – 1 Терабайт (Тбайт) = 1024 Гбайт = 240 байт, – 1 Петабайт (Пбайт) = 1024 Тбайт = 250 байт. Количеством информации называют ее числовую характеристику, отражающую ту степень неопределенности, которая исчезает после получения информации. Для оценки и измерения количества информации в сообщении применяются различные меры – синтаксическая, семантическая и прагматическая. При рассмотрении синтаксической меры информации выделяют два подхода – субъективный (статистический, вероятностный) и объективный (алфавитный). Статистический подход. Для количественной оценки неопределенности или энтропии Н Хартли Р. предложил формулу, содержащую логарифм от числа равновероятных возможностей N I = log 2 N, (1) которую можно записать в следующем виде: 2 I = N, (2) где I – количество информации или информативность события (в битах); N – число равновероятных событий (число возможных выборов). Минимальной единицей количества информации, именуемой битом, будет выбор из двух возможностей. Пример 1. При бросании монеты выбор одного результата (например, выпадения орла) несет один бит информации, поскольку количество возможных равновероятных результатов N = 2 (орел или решка). Действительно, подставляя N = 2 в формулу (1), получим I = 1 бит. Пример 2. Какой объем информации содержит сообщение, уменьшающее неопределенность в 4 раза? Решение: так как неопределенность знаний уменьшается в 4 раза, следовательно, она была равна 4, т.е. существовало 4 равновероятных события. Сообщение о том, что произошло одно из них, несет 2 бита информации (4 = 22). Ответ: 2 бита.
При не равновероятной возможности выбора количество информации, зависящей от индивидуальной вероятности i – го выбора, вычисляется по формуле К. Шеннона:
P – вероятность i -го выбора (отдельного события) рассчитывается:
где n – число нужных событий, N – общее число событий Если необходимо вычислить количество информации для всех событий с различными вероятностями (среднее значение количества информации), используют формулу:
Легко заметить, что если вероятности P1,..., PN равны, то каждая из них равна 1/N, и формула Шеннона превращается в формулу Хартли. Пример 3. В корзине лежат 8 черных шаров и 24 белых. Сколько информации несет сообщение о том, что достали черный шар? Дано: N, = 8; Nб = 24. Найти: Iч =? Решение: 1. N = 8 + 24 = 32 – шара всего; 2. Ответ: 2 бита. Алфавитный подход позволяет определить количество текстовой информации. Количество информации, которое несёт каждый символ вычисляется по формуле
где M – мощность алфавита, равная количеству символов в нем. Текст, содержащий К символов, имеет объем информации, равный:
где I – информационный вес (в битах) одного символа алфавита. Пример 4. В 2-символьном алфавите каждый символ несет 1 бит информации (M = 2, Пример 5. Объем сообщения, содержащего 2048 символов, составил 1/512 часть Мбайта. Каков размер алфавита, с помощью которого записано сообщение? 1/512 Мб=0,001953125 * 1024*1024*8=16384 бит I=16384/2048=8 бит M=2I= 28=256 символов
|

 (3)
(3)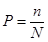 , (4)
, (4)
 – вероятность доставания черного шара; 3.
– вероятность доставания черного шара; 3. 
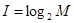 , (5)
, (5) (6)
(6)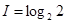 = 1 бит).
= 1 бит).


