Д3.1.
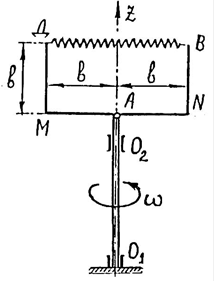
| Тонкие однородные стержни АNВ и АМД одинаковой массы, изогнутые под прямых углом, соединены в точке А шарниром. Стержни вращаются вокруг оси О1О2 с постоянной угловой, скоростью w. При этом они удерживаются в положении, при котором части МД и NВ параллельны, а АМ и АN перпендикулярны оси вращения, при помощи пружины ВД. Определить усилие в пружине.
|
Д3.2.

| Однородный полукруг массой т, радиусом R вращается с постоянной угловой скоростью w вокруг оси ОА. Определить реакции подшипника А и подпятника О. Расстояние от центра тяжести полукруга до оси ОА xc=4R/3p, где R - радиус.
|
Д3.3.
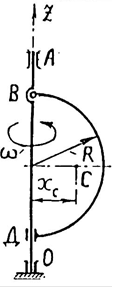
| Однородная проволочная полуокружность массой т, радиусом R вращается с постоянной угловой скоростью w вокруг оси ОА. Определить реакции в точках крепления В и Д кольца к оси ОА. Расстояние от центра тяжести полуокружности до оси ОА xc = 2R/3p.
|
Д3.4.

| Два тонких однородных стержня АВ и ДЕ одинаковой массы т скреплены невесомым стержнем С1С2 Стержень жёстко соединён с вертикальной осью O1O2, с которой он образует угол a. Стержни вращаются вокруг оси O1O2 с постоянной угловой скоростью w. Даны размеры: O1O = OO2 = b; С1O = OС2= l; AС1= С1B; ДС2 = С2Е. Определить реакции подпятника и подшипника.
|
Д3.5.

| Тонкое однородное проволочное кольцо массой т, радиусом R вращается с постоянной угловой скоростью w вокруг оси О, проходящей через его центр перпендикулярно его плоскости. Наибольшее усилие, которое выдерживает проволока при растяжении, равно S. С какой наибольшей угловой скоростью w может вращаться кольцо без разрыва? Расстояниеот центра О до центра тяжести полуокружности xc = 2R/3p.
|
Д3.6.

| Тонкий однородный стержень АВ массой т, лежащий в горизонтальной плоскости, вращается с постоянной угловой скоростью w вокруг вертикальной оси О, с которой он скреплен одинаковыми невесомыми стержнями ОА и ОВ длиной l. Определить реакции этих стержней.
|
Д3.7.

| Тонкий однородный стержень АВ массой т и длиной l вращается с постоянной угловой скоростью w вокруг вертикальной оси ОА. Стержень закреплен на оси при помощи шарнира А и невесомого стержня ВД; положение стержня АВ определяется углами a и b. Определить реакции связей стержня АВ.
|
Д3.8.

| Тонкий однородный стержень АВ длиной l вращается с постоянной угловой скоростью w вокруг вертикальной оси ОА. Вычислить угол отклонения стержня от вертикали, не учитывая трение в шарнире А. При каком наименьшем значении w стержень отклонится от вертикали?
|
Д3.9.

| Барабан лебедки радиусом г, установленной на жёсткой балке АВ, вращается с угловым ускорением e. Масса поднимаемого груза - m, момент инерции барабана лебёдки вместе с двигателем равен Jс, длина балки - l. Oпределить реакции заделки жёсткой консольной балки АВ. Массой каната и балки пренебречь.
|
Д3.10.
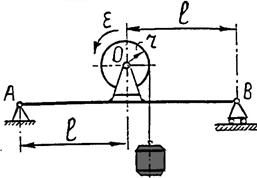
| Барабан лебедки радиусом r, установленной на жёсткой балке АВ, вращается с угловым ускорением e. Масса поднимаемого груза - m, масса лебедки - М. Пренебрегая массами каната и самой балки, определить реакции опор А и В. Центр тяжести О барабана находится на одинаковом расстоянии от опор А и В.
|
Д3.11.

| Клин В массой т опускается по поверхности клина А, образующей с горизонтом угол a. Определить давление клина А на горизонтальную плоскость, если его масса равна М.
|
Д3.12.

| Клин В массой т опускается по поверхности клина А, образующей с горизонтом угол a. Определить давление клина А на вертикальный выступ пола.
|
Д3.13.

| Ось колеса А массой т = 300 кг, радиусом r = 0,5 м движется с постоянной скоростью VА = 20 м/с. Центр тяжести С колеса смещен от его оси А на расстояние АС = h = 0,02 м. Определить давление колеса на рельс, когда его центр тяжести занимает наивысшее положение. Колесо катится без скольжения.
|
Д3.14.
| Тонкий однородный стержень АВ массой т, длиной l, закрепленный на оси О1О2 в точке А, вращается вокруг этой оси с постоянной угловой скоростью w, образуя с ней угол a. Определить усилие в пружине ВД.
|
Д3.15.

| Ось колеса А массой т = 300 кг, радиусом r = 0,5 м движется с постоянной скоростью VА = 20 м/с. Центр тяжести С колеса смещен от его оси А на расстояние АС = h = 0,02 м. Определить давление колеса на рельс, когда его центр тяжести занимает наинизшее положение. Колесо катится без скольжения.
|
Д3.16

| Тонкий однородный стержень АВ массой т, длиной 21, закрепленный шарнирно в своей середине О на оси O1O2, вращается вокруг этой оси с постоянной угловой скоростью w. При этом он удерживается в положении, образующем угол a с осью O1O2, при помощи пружины АД. Определить усилие в пружине.
|
Д3.17.
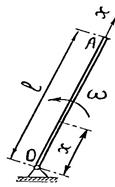
| Тонкий однородный стержень ОА массой т, длиной l вращается с постоянной угловой скоростью w вокруг вертикальной оси О. Определить продольное растягивающее усилие в сечении стержня в функции его координаты х.
|
Д3.18.

| Тонкие однородные стержни АВ и ДЕ массами т, на концах которых закреплены точечные грузы В и Е тоже массами т, вращаются вокруг неподвижной оси O1O2. Оба стержня перпендикулярны к оси вращения, причём АВ || 01у; ДЕ || 01х. Даны размеры: О1Д = ДА = АО2 =b; АВ = ДЕ = l. Определить реакции подпятника и подшипника.
|
Д3.19.
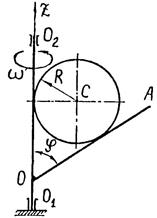
| Тонкий однородный и гладкий диск массой т, радиусом R установлен между валом O1O2. и стержнем ОА, приваренным к валу под углом j. Стержень и вал вращаются вместе с диском с постоянной угловой скоростью w. Определить давление диска на стержень и вал.
|
Д3.20.
| Невесомый стержень АВ длиной l, на конце которого расположен точечный груз В, вращается вокруг оси O1O2. с постоянной угловой скоростью w. Расстояние от шарнира А до оси вращения равно b. Определить значение w, если стержень отклонится от вертикали на угол j.
|