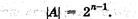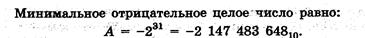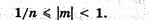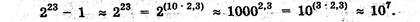Представление чисел в компьютере

Числовые данные обрабатываются в компьютере в двоичной системе счисления. Числа., хранятся в оперативной памяти в виде последовательностей нулей и единиц;, то есть в двоичном коде.

1. Представление чисел в формате с фиксированной занятой.

Целые числа в компьютере хранятся в памяти в формате с фик­сированной запятой. В атом случае каждому разряду ячейки памяти соответствует разрядной сетки.

Максимальное значение целого неотрицательного числа до­стигается в случае, когда во всех ячейках хранятся? единицы. Для n-разрядного представления они будет равно:

Пример. Определить диапазон, чисел, которые могут храниться в оперативной памяти в формате; целое неотрицательное число.

Минимальное число соответствует восьми нулям, храня­щимся в восьми ячейках памяти, и равно нулю.

Максимальное число соответствует восьми единицам, хранящимся в ячейках памяти и равно

A=1*2⁷+1*2⁶+1*2⁵+1*2⁴+1*2³+1*2²+1*2¹+1*2⁰=255₁₀

Диапазон изменения целых неотрицательных чисел от 0 до 255.

Для хранения целых чисел со знаком отводится две ячейки памяти (16 бит), причем старший (левый) разряд отводится под знак числа (если число положительное, то в знаковый раз­ряд записывается 0, если число отрицательное, то записывает­ся 1).

Представление в компьютере положительных чисел с исполь­зованием формата «знак-величина» называется прямым кодом

При представлении целых чисел в поразрядном представле­нии со знаком максимальное положительное число (с учетом выделения одного разряда на знак равно

Пример. Определить максимальное положительное чис­ло, которое может хранится в оперативной памяти в формате целое число со.знаком

А₁₀ = 2¹⁵ - 1= 32767.

Для представления отрицательных чисел используется дополнительный код. Дополнительный код позволяет заменить арифметическую операцию вычитания операцией сложения что существенно, упрощает работу процессора и увеличивает его быстродействие.

Дополнительный код отрицательного числа А, хранящегося в ячейках, равен 2ⁿ-[А|.

Дополнительный код представляет собой дополнение модуля отрицательного числа -А до 0, поэтому в n-разрядной компьютерной арифметике:

2ⁿ-[А|.+[А|=0

Это равенство тождественно справедливо, так как в компью­терной n-разрядной арифметике 2ⁿ =0 Действительно, двоич­ная запись такого числа состоит из одной единицы и п нулей, а в n-разрядную ячейку может уместиться только n младших разрядов, то есть n нулей.

Проведем проверку с использованием десятичной системы счисления. Дополнительный код 63§34ю в сумме/с модулем от­рицательного числа 2002₁₀ равен 65536₁₀), то есть дополнитель­ный код дополняет модуль отрицательного числа до 2¹⁶ (до нуля 16-разрядной компьютерной арифметики).

Для получения дополнительного кода отрицательного числа можно использовать довольно простой алгоритм:

1. Модуль числа записать прямым кодом в п двоичных раз­рядах;

2. Получить обратный код числа для этого значения всех бит инвертировать (все единицы заменить на нули и все нули заменить на единицы);,

3. К полученному обратному коду прибавить единицу.

При n-разрядном представлении отрицательного числа А до­полнительным кодом старший разряд выделяется для хране­ния знака числа (единицы). В остальных разрядах записывается положительное число:

Чтобы число было положительным, должно •выполняться условие:

Следовательно, максимальное значение модуля числа А в n-разрядном представлении

Тогда минимальное отрицательное число равно:

Пример. Определить диапазон чисел, которые могут храниться в оперативной памяти в формате больших целых чи­сел со знаком (для хранения таких чисел отводится четыре ячейки памяти — 32 бита).

Максимальное положительное целое число (с учетом выделе­ния Одного разряда на знак) равно:

Достоинствами представления чисел в формате с фиксиро­ванной запятой являются простота и наглядность представле­ния чисел, а также простота алгоритмов реализации арифме­тических операций (вычитание благодаря использованию дополнительного кода для представления отрицательных; чисел сводится к сложению).

Сложим прямой код положительного числа с дополнитель­ным кодом отрицательного числа. Получим результат в допол­нительном коде:

Недостатком представления чисел в формате с фиксирован­ной запятой является конечный диапазон представления вели­чин, недостаточный для решения математических, физиче­ских, экономических и других задач, в которых используются как очень малые, так и очень большие числа.

 

2. Представление чисел в формате с плавающей запятой.

Ве­щественные числа (конечные и бесконечные десятичные дроби) хранятся и обрабатываются в компьютере в формате с плаваю­щей запятой. В этом случае положение запятой в записи числа может изменяться.

Формат чисел с плавающей запятой базируется на экспо­ненциальной форме записи, в которой может бить представле­но любое число. Так, Число А может быть представлено в виде:

Для однозначности представления чисел с плавающей запя­той используется нормализованная форма, при которой ман­тисса отвечает условию:

Это означает, что мантисса Должна быть правильной дробью и иметь после запятой цифру, отличную от нуля.

Число в форме с плавающей запятой занимает в памяти компьютера четыре (число обычной точности) или восемь байтов (число двойной точности). При записи числа с плавающей запятой выделяются разряда! для Хранения знака мантиссы, знака порядка, порядка и мантиссы.

Диапазон изменения чисел определяется количеством разрядов, отведенных для хранения порядка числа, а точность (ко­личество значащих цифр) определяется количеством разрядов, отведенных для хранения 'мантиссы.

Точность вычислении определяется количеством разрядов, от­веденных для хранения мантиссы чисел. Максимальное значение положительной мантиссы равно:

При сложении и вычитании чисел в формате с плавающей за­пятой сначала производится подготовительная операция выравнивания порядков. Порядок меньшего (по модулю) числа увели­чивается до величины порядка большего по модуля числа. Для того чтобы величина числа не изменилась, мантисса уменьшается в такое же количество раз (сдвигается в ячейке памяти вправо на количество разрядов, равное разности порядков чисел).

После выполнения операции выравнивания одинаковые раз­ряды чисел оказываются расположенными в одних и тех же разрядах ячеек памяти. Теперь операций сложения и вычитания чисел сводятся к сложению или вычитанию мантисс.

После выполнения арифметической операции для приведе­ния полученного числа к стандартному формату с плавающей запятой производится нормализация, т.е. мантисса сдвигается вправо или влево так, чтобы ее значащая цифра попала в первый разряд после запятой.

Приумножении чисел в формате с плавающей запятой по­рядки складываются, а мантиссы перемножаются»: При деле­нии из порядка делимого вычитается порядок делителя, а мантисса делимого делится на мантиссу делителя.