Алгебра высказываний. Алгебра в широком смысле этого слова — наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над различными математическими
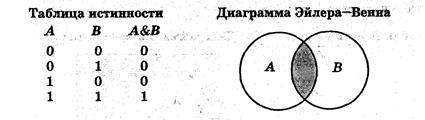
Алгебра в широком смысле этого слова — наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над различными математическими объектами (алгебра переменных и функций, алгебра векторов, алгебра множеств и так далее). Объектами алгебры логики являются высказывания. Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт — истинно или ложно данное высказывание, что дает возможность определять истинность или ложность составных высказываний алгебраическими методами. Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами: А = {Аристотель — основоположник логики}; В ={На яблонях растут бананы}. Истинному высказыванию ставится в соответствие 1, ложному — 0. Таким образом, А =1, В = 0. Составные высказывания на естественном языке образуются с помощью союзов, которые в алгебре высказываний заменяются на логические операции. Логические операции задаются таблицами истинности и могут быть графически проиллюстрированы с помощью диаграмм Эйлера-Венна. Логическая операция КОНЪЮНКЦИЯ (логическое умножение): • в естественном языке соответствует союзу и; • в алгебре высказываний обозначение &; • в языках программирования обозначение And. Конъюнкция — это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являются истинным тогда и только тогда, когда оба исходных высказывания истинны. i В алгебре множеств конъюнкции соответствует операция пересечения множеств, то есть множеству, получившемуся в результате умножения множеств А и В, соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение): • в естественном языке соответствует союзу или; • обозначение у; • в языках программирования обозначение Or. Дизъюнкция — это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно. В алгебре множеств дизъюнкции соответствует операция объединения множеств, то есть множеству, получившемуся в' результате сложения множеств А и В, соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.
Логическая операция ДИВЕРСИЯ (отрицание): • в естественном языке соответствует словам неверно, что... и частице не; • обозначение А; • в языках программирования обозначение Not. Отрицани е – это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том» что исходное высказывание отрицается.; В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, то есть множеству, получившемуся в результате отрицания множества А, соответствует множество А, дополняющее его до универсального множества.
Логическая операция ИМПЛИКАЦИЯ (логическое следование): • в естественном языке соответствует обороту если..., то...; • обозначением. Импликация — это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие.(второе высказывание) ложно.
Логическая операция ЭКВИВАЛЕНЦИЯ (равнозначность): • в естественном языке соответствует оборотам речи тогда и только тогда; в том и только в том случае; • обозначения <=>, Эквиваленция — это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны. Таблица истинности эквиваленции:
Логические операции имеют следующий приоритет: действия в скобках, инверсия, &, v, =>, <=>.
|