Определение дисконтированного чистого дохода
(или "чистой текущей стоимости" - net present value) Рассмотрим последовательность годовых затрат и доходов (выручки) за период от t = 0 до t = n. - Выручка: Во, Bi,..., Вn - Затраты: 3o,3i,..., Зn Для оценки результатов можно было бы суммировать всю выручку и вычесть суммарные затраты. Но такой подход имеет тот недостаток, что придает одинаковую значимость (ценность) 1 руб., получаемому через n-лет и 1 руб., получаемому сегодня, в то время как эти альтернативы далеко не равнозначны. Действительно, 1 руб., получаемый через n-лет эквивалентен сумме S, которую необходимо было бы иметь сегодня, чтобы получить один руб. через n-лет: для определения этой суммы S предположим, что на "рынке капиталов" 1 руб. сегодня обменивается на (1+ii) руб. через год: эта норма обмена или процентная ставка равна i2 в следующем году и т.д. Следовательно, сумма S, вложенная сегодня, обеспечит: S (1+ii) в конце первого года S (l+ii)(l+i2) в конце второго года S (l+ii)(l+i2)*...*(l+in) в конце n-го года так что для получения 1 руб. через n лет необходимо вложить сегодня:
Сумма S называется "дисконтированной" или "текущей стоимостью" перспективы получения 1 руб. через n лет. Поэтому "дисконтированная сумма чистых доходов", соответствующая рассматриваемой последовательности ожидаемой выручки и затрат, задается выражением:
С целью упрощения расчетов норму процента i положим постоянной: i 1 = i 2 =... = in = i. Тогда:
Для сравнения двух решений долгосрочного периода, (инвестиционных проектов) характеризующихся некоторой последовательностью выручки и затрат используется критерий "дисконтированного чистого дохода" (ДЧД). Предпочтение отдается проектам с наибольшей величиной D. Примеры расчета. Начальные инвестиции обозначим через I. За период от года t=l до года n они обеспечивают постоянную величину валовой прибыли (выручки за вычетом эксплутационных затрат) в размере R. Дисконтированный чистый доход от этих инвестиций составит:
или после упрощений: Примем следующие исходные данные: 1 = 8 млн. руб. R= 1 млн. руб. i = 8 %
В зависимости от срока функционирования проекта капитальных вложений имеем: для n = 12 лет: D = – 0,46: капитальные вложения отвергаются; для n = 20 лет: D = +1,82: капиталовложения рентабельны. При стремлении n к бесконечности дробь (1 / (l + i)) N стремится к нулю, поскольку 1/(1+ i) < 1. Выбор нормы и периодов дисконтирования. а) Выбор нормы диcконтирования В настоящее время все еще слабо развит «рынок капиталов», который бы позволял определить на основе сравнения спроса на кредитные ресурсы и предложения кредита единственное значение процентной ставки I, пригодной для всех организаций. В действительности условия кредита существенно различны в зависимости от финансового института, являющегося заимодавцем. Кроме того, они зависят от степени риска вложений, продолжительности возмещения кредита. Так, норма процента для долгосрочных рискованных проектов выше, чем для краткосрочных. Наконец, учет возможного обесценивания денег играет определенную роль в формулирование условий кредита. Вследствие этого норма дисконта, используемая экономистами не столько отражает рыночную норму процента, сколько относительную значимость для фирмы оцениваемых будущих доходов в сравнении с текущими доходами (или затратами - отрицательными доходами). В качестве нормы дисконтирования часто используется средневзвешенная величина стоимости инвестиций по различным источникам их финансирования. Пусть, например, 80% процентов инвестиций финансируется за счет банковских кредитов под 8% годовых (в постоянных ценах), а 20% - за счет собственных ресурсов с нормой предельной рентабельности 12%. Тогда средневзвешенная норма дисконта для хозяйствующего субъекта составит:
На практике при обосновании производственных и управленческих решений инженер-экономист может выбрать среднюю процентную ставку в качестве нормы дисконта (-10%) и затем проанализировать чувствительность получаемых результатов в зависимости от выбранной нормы. б) Выбор периода дисконтирования. Эффект от капитальных вложений проявляется для достаточно длительного планового горизонта, но фактически процедура дисконтирования обуславливает сравнительно малый "вес", затрат и результатов удаленных периодов (сглаживая тем самым недостаточную точность прогнозирования удаленных затрат и эффектов). Поэтому можно выбрать "срок службы" производственных фондов n меньше его теоретического значения. При этом не корректно сравнивать дисконтированные доходы, в случае если рассматриваемые проекты имеют различные сроки функционирования n.
Внутренняя норма рентабельности (ВНР). Для ее определения обратимся к численному примеру, в котором начальные инвестиции I обеспечивают постоянную годовую прибыль R в течение n лет. Величина ДЧД, обеспечиваемая инвестициями, составит:
Из этого выражения следует, что дисконтированный доход убывает с ростом нормы дисконта i. Так, для I = 8 млн. руб. R = 1 млн.руб. n = 20 лет и для нормы дисконта 1 = 8 % находим: Это свойство убывания ДЧД с ростом нормы дисконта i имеет общий характер. Оно обусловлено тем, что удаленные во времени результаты оказывают тем меньшее влияние на начальные затраты, чем выше норма дисконта. Из этого свойства следует, что величина ДЧД обычно положительна для малых значений нормы дисконта, и отрицательна для больших его значений, обращаясь в нуль для некоторой конкретной величины i* = r. Последняя называется "средней" или "внутренней" нормой рентабельности инвестиций. Для этой нормы проект вложений представляет собой нейтральную операцию, поскольку для нее ДЧД = 0. Для иллюстрации обратимся к нашему примеру, приняв n = 00. В этом случае дисконтированный чистый доход составит:
Величина r, для которой ДЧД = 0 определится из условия: 0 = –I +R/r. Отсюда: r = R/I Так, например, для I = 8 млн. руб. и R = 1 млн. руб. имеем: для i = 8 %: для i = R / I = 1/8 = 12,5 %: для i > 12,5 %
Таким образом: норма рентабельности инвестиций r определяется как норма процента, для которой величина ДЧД от инвестиций равна нулю. Для i < r, Для I > r, В результате для приобретения финансовых ресурсов фирма согласна платить максимальную процентную ставку, равную ВНР. Норму рентабельности используют для сравнения проектов инвестиций, хотя более корректный критерий - дисконтированный чистый доход. Причина заключается в том, что для расчета величины ДЧД необходимо знать норму дисконта, что представляет непростую задачу для организации. Напротив, внутренняя норма рентабельности может быть рассчитана без знания нормы дисконта.
Критерий средних дисконтированных затрат (СДЗ) Для сравнения двух проектов капитальных вложений можно использовать средние дисконтированные затраты, рассчитываемые по следующей формуле:
где З0, 31, З2,..., З n – затраты, обусловленные произведенными инвеcтициями; Q0, Q1, Q2,..., Q n - годовой выпуск продукции, получаемый за счет инвестиций (Q0- выпуск нулевого года, в момент вложений, как правило, равен нулю). Сравнение двух вариантов капитальных вложений с помощью критерия средних дисконтированных затрат эквивалентно сравнению по критерию ДЧД при условии, что эти доходы рассчитываются для неизменных во времени цен. Рассчитанные таким образом средние приведенные затраты равны минимальной цене реализации продукции, для которой капитальные вложения оказываются рентабельными. Иногда этот показатель называют "ценой производства" для рассматриваемого варианта капитальных вложений. Показатель средних дисконтированных затрат удобен на практике, хотя и представляет лишь модификацию критерия ДЧД.
Среднегодовая эквивалентная прибыль. Для некоторых частных случаев расчет ДЧД можно заменить определением среднегодовой прибыли, исчисленной без амортизационных отчислений и процентов. Пусть К0 - первоначальные затраты на сооружение объекта или на закупку оборудования. Годовые величины прибыли (валового дохода за вычетом текущих затрат) составляют U 1, U 2,..., U n. Суммарный дисконтированный эффект от капиталовложений будет равен:
Постоянная годовая величина эффекта X, обеспечивающая полное возмещение капитальных вложений за весь срок их службы составит:
отсюда Если годовая прибыль постоянна U 1 = U 2 =... = Un = U, то величина X соответствует годовой оценке капитальных затрат, состоящих из амортизационных отчислений и процентов. Годовую эффективность проекта можно оценить, вычислив разность U – X. Такая оценка эквивалентна оценке на базе ДЧД. Поэтому сравнение нескольких видов оборудования может производиться как на базе расчета ДЧД, так и с использованием общепринятого и более понятного показателя годовой чистой прибыли за вычетом амортизационных отчислений и процентов. Последний метод расчета имеет то преимущество, что позволяет оценить варианты, имеющие различный срок службы, в то время как для таких капитальных вложений прямое их сравнение, исходя из величины чистой прибыли, оказывается невозможным. Сумма амортизационных отчислений и процентов задается величиной X, которую можно назвать постоянной годовой выплатой (аннуитетом), позволяющей возместить за n лет с нормой дисконта i первоначальные вложения К0. Критерий сравнительной рентабельности (КСР). КСР - это отношение дисконтированной прибыли к дисконтированным инвестициям. Ни одна из компаний не обладает неограниченным капиталом для финансирования проектов. Одним из методов, позволяющих сделать выбор наиболее рентабельного проекта является использование показателя КСР:
Дисконтирование должно производиться с нормой реинвестирования компании. Учет инфляции. Расчеты критериев рентабельности можно проводить в текущих (инфляционных) или в постоянных ценах, т.е. ценах начального года. При расчетах в текущих ценах - инфляционный денежный поток дисконтируется с нормой реинвестирования (дисконта) компании; - поток наличности дисконтируется с темпом инфляции валюты, принятой в расчетах. То есть, коэффициент дисконтирования будет равен: (1 + норма дисконта компании)*(1 +процент инфляции) Например: - норма реинвестирования компании 10% - прогнозные темпы инфляции 5% Тогда потоки денежной наличности будут дисконтироваться с нормой: 1.10 ×1.05= 1.555 или 15.5%. Расчет в постоянных ценах целесообразен в тех случаях, когда темпы инфляции затрат и цен на продукцию (услуги) достаточно близки или когда прогноз инфляции очень затруднителен и не определен.
|

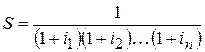 . (7.1)
. (7.1) . (7.2)
. (7.2)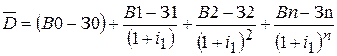 . (7.3)
. (7.3) (7.4)
(7.4)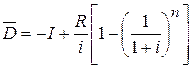 . (7.5)
. (7.5) . (7.6)
. (7.6)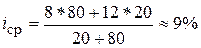 .
.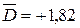 . При тех же исходных данных, но для 1 = 10 %, имеем
. При тех же исходных данных, но для 1 = 10 %, имеем 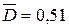 .
.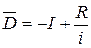 . (7.8)
. (7.8)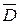 = – 8 + 1/0,08 = – 8 +12,5 = 4,5 млн.руб.
= – 8 + 1/0,08 = – 8 +12,5 = 4,5 млн.руб.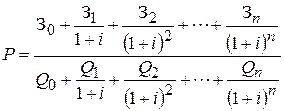 , (7.9)
, (7.9)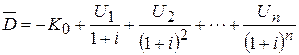 . (7.10)
. (7.10)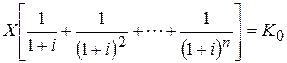 ,
,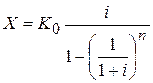 . (7.11)
. (7.11)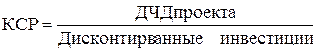 . (7.12)
. (7.12)


