Практическая работа №2. Получить практические навыки при кодировании данных в различных системах счисления.
Тема: Системы счисления.
Цель работы: Получить практические навыки при кодировании данных в различных системах счисления.
Теоретическая часть: В ЭВМ информация представлена в виде двоичных чисел. За основу взято два устойчивых состояния (лампочка включена или выключена, намагничен сердечник или не намагничен и т.д.). Принято одно состояние обозначать 1, а другое 0. Эти числа называются двоичными или битами (binary digit – двоичная цифра). Для кодирования одной буквы или одного знака требуется 8 бит, что составляет 1 байт – это общепринятая единица измерения информации. В двоичном кодировании можно закодировать 256 символов. Существуют и более крупные единицы измерения количества информации: 1 байт = 8 бит 1 Кбайт (килобайт) = 1024 байт 1 Мбайт (мегабайт) = 1024 Кбайт 1 Гбайт (гигабайт) = 1024 Мбайт. Вообще для записи чисел, нужно обязательно использовать какую-либо систему счисления, которая показывает, по каким правилам мы записываем числа и выполняем над ними действия. Общепринятая десятичная система счисления является позиционной, то есть значение любой цифры числа определяется не только самой цифрой, но и ее позицией (местом), которое она занимает. В десятичной системе счисления в каждой единице следующего разряда содержатся 10 единиц предыдущего разряда. Это соотношение единиц соседних разрядов, называется основанием системы счисления. Следовательно, основанием десятичной системы счисления является число 10. В ЭВМ применяются позиционные системы счисления: непозиционные (например, римская система счисления) в ЭВМ не используются из-за своей громоздкости и сложности правил образования.
Пример перевода числа из двоичной в десятичную систему счисления: Любое число из двоичной системы счисления может быть переведено в десятичную при помощи развернутого вида числа: 10001012 = 1*26+0*25+0*24+0*23+1*22+0*21+1*20 = 6910. При переводе двоичных дробей, степень основания развернутого вида числа берется с отрицательным знаком: 0,012 = 0*2-1 + 1*2-2 = 0 + 1*1/4 = 0,2510.
Пример перевода числа из двоичной в восьмеричную систему счисления: Двоичное число надо разбить на триады справа налево и, пользуясь таблицей, записать двоичные триады в 8-ричном представлении: 11010102 = Дробные числа разбиваются на триады справа налево – целая часть числа и слева направо – дробная часть числа: 1101,10012 =
Пример перевода числа из двоичной в шестнадцатеричную систему счисления: Двоичное число разбиваем на тетрады справа налево и, пользуясь таблицей, записываем двоичные тетрады в 16-ричном представлении: Дробные числа разбиваются на тетрады справа налево – целая часть числа и слева направо – дробная часть числа: 100111,11100112 = 0010 0111,1110 01102 = 27,E616.
Пример перевода числа из восьмеричной в десятичную систему счисления: Восьмеричная система счисления имеет основание 8 и цифры 0, 1, 2, 3, 4, 5, 6, 7. Здесь, также как и в двоичной системе счисления, любое число может быть переведено в десятичную систему счисления при помощи развернутого вида числа: (726,15)8 = 7*82+2*81+6*80+1*8-1+1*8-2 = (470,13/64)10
Пример перевода числа из восьмеричной в двоичную систему счисления: По таблице записываем 8-ричные цифры двоичными триадами: 528 = 101 010 = 1010102
Пример перевода числа из восьмеричной в шестнадцатеричную систему счисления: По таблице записываем 8-ричные цифры двоичными триадами, затем разбиваем на тетрады справа налево и также, пользуясь таблицей, записываем тетрады в 16-ричном представлении: 528 = 1010102 = 2А16
Пример перевода числа из шестнадцатеричной в десятичную систему счисления: Шестнадцатеричная система счисления имеет основание 16 и цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F. Здесь, также как и в предыдущих системах счисления, любое число может быть переведено в десятичную систему счисления при помощи развернутого вида числа: (10A,F)16 = 1*162+0*161+10*160+15*16-1 = (266,15/16)10
Пример перевода числа из шестнадцатеричной в двоичную систему счисления: Каждую цифру 16-ричного числа записываем 2-ичной тетрадой по таблице: 2А16 = 0010 10102 = 1010102
Пример перевода числа из шестнадцатеричной в восьмеричную систему счисления: Аналогично, записываем 16-ричное число 2-ичными тетрадами, затем разбиваем полученное 2-ичное число на триады справа налево и по таблице записываем каждую двоичную триаду 8-ричным числом: 2А16 = 1010102 = 528
Пример перевода числа из десятичной в двоичную систему счисления: Десятичная система счисления имеет основание 10 и цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Перевод чисел из 10-тичной с/с в 2-ичную, 8-ричную, 16-ричную и какую-либо другую систему счисления осуществляется с помощью деления в столбик десятичного числа на основание той системы счисления, в которую нужно перевести. Остатки от деления записываются справа налево, и полученная запись чисел является результирующим числом. Перевод числа 65 в восьмеричную систему счисления:
Особенности перевода 10-тичных дробей: Перевести 0,2510 в 2-ичную и 8-ричную системы счисления. Здесь всегда умножается только дробная часть числа, если множимое число больше или равно 5, то в результате пишем 1, если меньше 5 – пишем 0. 0,25*2 = 0,5 | 0 0,25*8 = 2,00 | 2 0,5*2 = 1,00 | 1 0,2510 = 0,012 0,2510 = 0,28
Порядок выполнения работы: 1. Внимательно изучите теоретическую часть работы. 2. Получите у преподавателя свой вариант выполнения задания. 3. Подготовьте отчет. Отчёт по практической работе №2 Тема: Цель работы: Выполнение работы:
Вывод: Практическая работа №3
Тема: Представление различных видов информации на компьютере.
Цель работы: Изучить принципы кодирования различных видов информации.
Теоретическая часть:
|

 = 1528.
= 1528.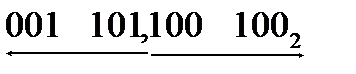 = 15,448.
= 15,448. = 0110 10102 = 6А16.
= 0110 10102 = 6А16.


