Теплоёмкость идеального газа.
Для того чтобы воспользоваться формулами (63,64) найдем значения входящих в них частных производных из уравнения Менделеева-Клапейрона. Pv=RT Продифференцируем это уравнение p dv + v dp = R dT, откуда имеем
В предыдущем параграфе было получено
Таким образом, внутренняя энергия идеального газа от величины объёма не зависит, т.е. U¹U(v). Исследуем вопрос зависимости внутренней энергии идеального газа от величины давления.
Из (68) следует, что U≠U(P) Таким образом, внутренняя энергия идеального газа не зависит от величины давления, следовательно, внутренняя энергия идеального газа зависит только от температуры газа. Внутренняя энергия- это функция состояния, поэтому dU- дифференциал функции состояния. Любая функция состояния может быть выражена через любое сочетание термодинамических параметров состояния системы. Внутренняя энергия может быть выражена как U=U(T,v), по правилам математики полный дифференциал функции двух переменных запишется следующим образом:
Так как dU = cv dT откуда
Для идеального газа полная производная изменения внутренней энергии определяется Для того чтобы взять интеграл нужна связь между Cv и Т. Если в диапазоне температур T1 и T2, cv взять средним значением, то DU = А абсолютное значение запишется:
где U0 – постоянная интегрирования. Массовая изобарная теплоёмкость идеального газа определяется из формулы (63)
После подстановки (65,66) в (63) получим
Окончательно:
Формула (74)- уравнение Майера. Из этой формулы следует, что массовая изобарная теплоёмкость больше на величину удельной газовой постоянной (R) массовой изохорной теплоёмкости идеального газа. В случае мольных теплоёмкостей уравнение Майера запишется в виде:
где Rm = 8314 из формулы (75) следует, что молярная изобарная теплоемкость больше молярной изохорной теплоемкости на величину универсальной газовой постоянной. Обозначим через K- Показатель адиабаты (коэффициент Пуассона). K, показывает во сколько раз изобарная теплоемкость больше изохорной. Так как по уравнению Майера изобарная теплоемкость всегда больше изохорной, то K всегда больше единицы (K>1). Как показали эксперименты, с ростом температуры показатель адиабаты слабо убывает поэтому в инженерных расчетах показатель адиабаты берут в среднем значении так для двухатомных газов, включая воздух который на 79% состоит из N2 и примерно на 21% из О2, берется значение K»1,4.
|

 (65)
(65) (66)
(66) - справедливо для реального и идеального газа. Подставим в это выражение значение
- справедливо для реального и идеального газа. Подставим в это выражение значение  для идеального газа:
для идеального газа: (67)
(67) , где
, где  - изотермическая сжимаемость, которая является конечной величиной, т.е.
- изотермическая сжимаемость, которая является конечной величиной, т.е.  .
. (68)
(68) (69)
(69) (61)
(61) таким образом, для идеального газа получаем
таким образом, для идеального газа получаем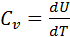 (70)
(70)
 (T2-T1) (72)
(T2-T1) (72) (73)
(73) , из формул (65,66) частные производные:
, из формул (65,66) частные производные:
 (74)
(74) (75)
(75)
 (76)
(76)


