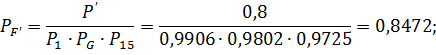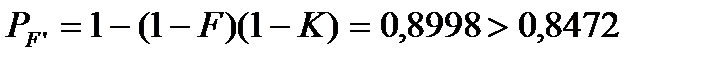Задание 1
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение Высшего профессионального образования «Уфимский государственный нефтяной технический университет»
Кафедра автоматизация технологических процессов и производств
Курсовой проект
по курсу «Диагностика и надежность АС»
На тему «Расчет надежности информационной системы»
Вариант 3
Выполнил: студент гр. БАГ-09 Зиапов А.Ф.
Проверил: Ишинбаев Н.А.
Уфа 2013
Содержание с. 1. Задание 1........................................................................................................2 2. Задание 2......................................................................................................11 Список используемой литературы..................................................................14
Задание 1 По структурной схеме надежности информационной системы и заданным значениям интенсивности отказов ее элементов: 1) построить график изменения вероятности безотказной работы системы от времени наработки в диапазоне снижения вероятности до уровня 0,1 – 0,2; 2) определить время наработки системы соответствующее заданному γ (гамма-процентному ресурсу системы); 3) обеспечить при заданном γ (гамма-процентном ресурсе) увеличение времени наработки системы не менее чем в 1,5 раза за счет структурного резервирования элементов системы. Исходные данные: Таблица 1. Исходные данные.
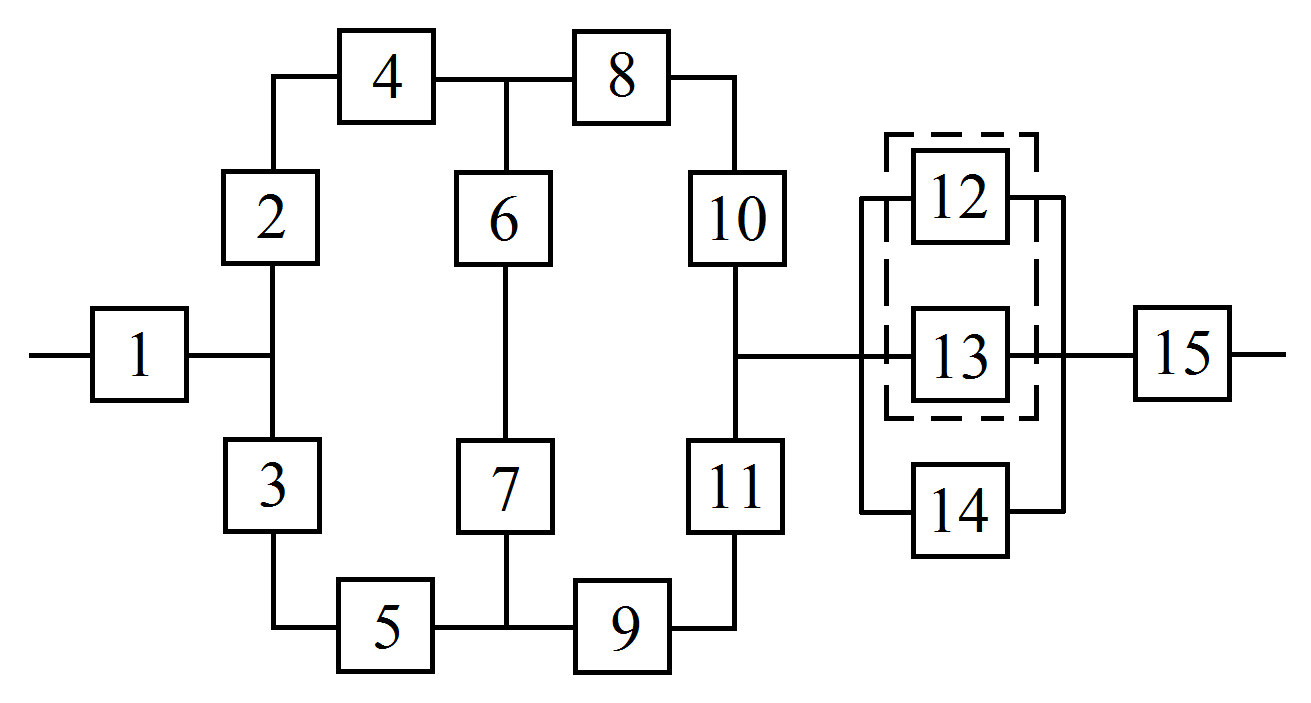
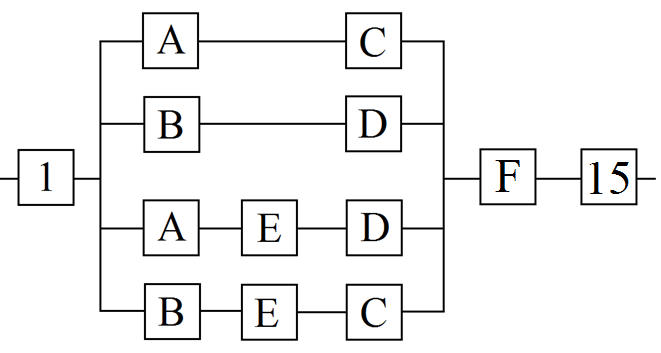
Рисунок-1 - Структурная схема
Значения интенсивности отказов элементов составляют: λ1 = 0,1∙10-6 1/ч, λ2 = λ3 = λ4 = λ5 = λ8 = λ9 = λ10 = λ11 =1,0∙10-6 1/ч, λ6 = λ7 =2,0∙10-6 1/ч, λ12 = λ13 = λ14 =5,0∙10-6 1/ч, λ15 =0,2∙10-6 1/ч, γ = 80%. γ – (гамма-процентный ресурс системы) – вероятность безотказной работы системы, выраженный в процентах, по истечении определенного времени непрерывной работы (наработки) системы. Все элементы системы работают в режиме нормальной эксплуатации. Расчет: 1. В исходной схеме элементы 2 и 4 - образуют последовательное соединение. Заменяем их квазиэлементом А: PA= P2∙ P4. (1) 2. Элементы 3 и 5 образуют последовательное соединение. Заменяем их квазиэлементом B: PB=P3∙P5. (2) 3. Элементы 8 и 10 образуют последовательное соединение. Заменяем их квазиэлементом C: PC=P8∙P10. (3) 4. Элементы 9 и 11 образуют последовательное соединение. Заменяем их квазиэлементом D: PD=P9∙P11. (4) 5. Элементы 6 и 7 образуют последовательное соединение. Заменяем их квазиэлементом E: PE=P6∙P7. (5) 6. Элементы 12, 13 и 14 образуют соединение «2 из 3», которое заменяем элементом F. Так как p 12 = p 13 = p 14, то для определения вероятности безотказной работы элемента F можно воспользоваться выражением, в основе которого лежит формула биноминального распределения (биноминальному распределению подчиняется дискретная случайная величина k – число появлений некоторого события в серии из n опытов, если в отдельном опыте вероятность появления события составляет p).
где
Поскольку для отказа системы «m из n» достаточно, чтобы количество исправных элементов было меньше m, вероятность отказа может быть найдена по теореме сложения вероятностей для k = 0,1, …,(m – 1):
Аналогичным образом можно найти вероятность безотказной работы как сумму для k = m, m + 1, …, n:
В данном конкретном случае, при n = 3 и m = 2,вероятность безотказной работы элемента A определится выражением:
После преобразований схема примет вид:
Рисунок-2 - Преобразованная схема. 7. Элементы A, B, C, D и E, изображенные на Рисунке-2 образуют мостиковую систему, которую можно заменить квазиэлементом G. Для расчета вероятности безотказной работы воспользуемся методом минимальных путей. Логическая схема мостиковой системы по методу минимальных путей приведена на Рисунке-3:
Рисунок-3 – Преобразованная мостиковая схема 8. Система, изображенная на рисунке 3 работоспособна до тех пор, пока работоспособны элементы A и C или – B и D или – A, E и D или – B, E и C. C учетом PA=PB=PC=PD, вероятность работы квазиэлемента G определяется по формуле:
После преобразования схема примет вид:
Рисунок-4 - Преобразованная схема. 9. В преобразованной схеме элементы 1, G, F и 15 образуют последовательное соединение. Тогда вероятность безотказной работы всей системы будет определяться следующим выражением: P= P1∙ PG∙ PF∙ P15 (8) Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 15 подчиняются экспоненциальному закону:
10. Результаты расчетов вероятностей безотказной работы элементов 1 – 15 исходной схемы по формуле (9) для наработки до 0,22·106 часов представлены в таблице 1. Таблица 2. Вероятности элементов для наработки
11. Результаты расчетов вероятностей безотказной работы всех элементов системы для наработки до 0,22∙106 часов представлены в таблице 2. 12. На рисунке 5 представлен график зависимости вероятности безотказной работы системы Р от времени t. 13. По графику находим для γ = 80% (Р= 0,8) γ- процентную наработку системы t= 0,0627∙106 ч. 14. Проверочный расчет при t= 0,0627∙106 ч. показывает, что Pγ= 0,8002~ 0,8. 15. По условиям задания находим время, превышающее в 1,5 раза время, соответствующее вероятности безотказной работы. t’= 1,5∙0,0627∙106 =0,0941∙106 ч. 16. Расчет показывает, что при t’= 0,0941∙106 ч. для элементов преобразованной схемы P1(t’)=0,9906, P15(t’)=0,9802, PG(t’)=0,9725 и PF(t’)=0,6832. Следовательно, из четырех последовательно соединенных элементов минимальное значение вероятности безотказной работы имеет элемент F, и именно увеличение его надежности даст максимальное увеличение надежности системы в целом. 17. Для того чтобы при t’= 0,0941∙106 ч. система в целом имела вероятность безотказной работы P’=0,8, надо найти необходимую вероятность безотказной работы элемента F: P’= P1∙ PG∙ PF’∙ P15 где PF’ – необходимая вероятность безотказной работы элемента F.
- добавляем элемент K, получаем:
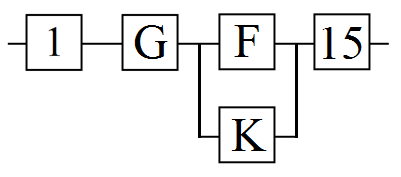
19. Таким образом, для повышения надежности до требуемого уровня, необходимо к элементу F добавить один резервный элемент К. Резервированная система изображена на Рисунке-5.
Рисунок-5 - Схема с повышенной надежностью. 12. Расчеты показывают, что при t’= 0,0941∙106 ч., Р’ = 0,8505> 0,8, что соответствует условию задания.
Рисунок-6 - График зависимости вероятности безотказной работы системы P и P’ от времени (наработки) t.
Вывод: 1. По данным расчета вероятности безотказной работы системы от времени построен график P(t). 2. По графику найдено время, соответствующее 80% - процентному ресурсу системы (t = 0,0627 × 106 ч). 3. Для увеличения наработки системы в 1,5 раза при 80% g -процентном ресурсе системы предложено нагруженное резервирование основного элемента F, идентичным по надежности резервным элементом K. 4. Рассчитана вероятность безотказной работы системы с повышенной надежностью от времени, построен график P’(t) системы с повышенной надежностью.
|

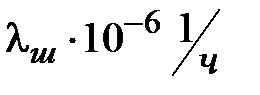 Интенсивности отказов элементов, х10-6 1/ч
Интенсивности отказов элементов, х10-6 1/ч
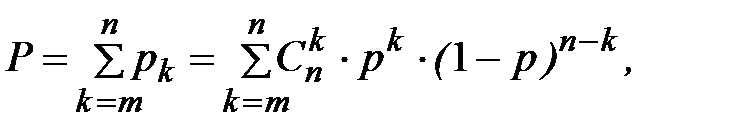
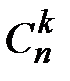 –биноминальный коэффициент, называемый «числом сочетаний по k из n» (т. е. сколькими разными способами можно реализовать ситуацию k из n).
–биноминальный коэффициент, называемый «числом сочетаний по k из n» (т. е. сколькими разными способами можно реализовать ситуацию k из n).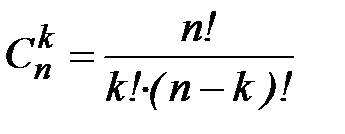 .
.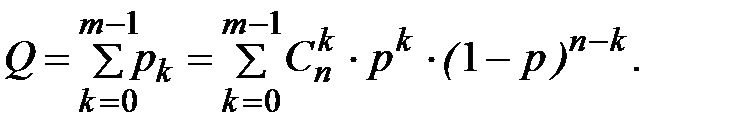
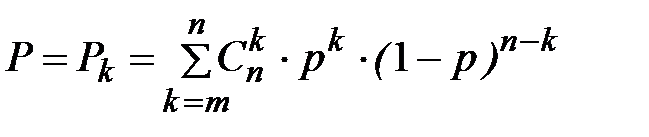 .
.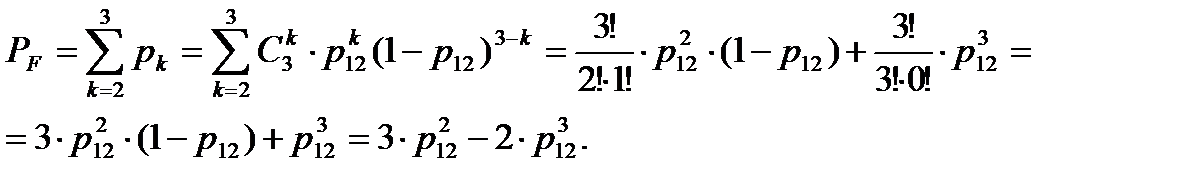 (6)
(6)
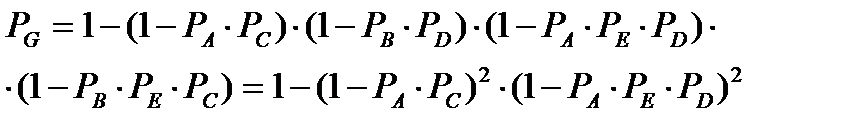 (7)
(7)
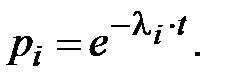 (9)
(9)