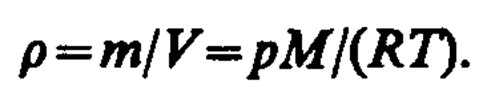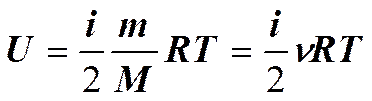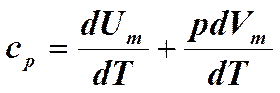Классическая статистика. Функция распределения Максвелла. Барометрическая формула. Распределение Больцмана.
Компьютерная верстка Ю.В. Одинцова Б.Б. Кузнецова Издательство ООО «Фирма «ИНКОС» 04116, г.Киев, ул. Маршала Рыбалка, 10/8 тел.: (044) 206-47-21, 206-47-29,481-28-77 e-mail: inkos@In.ua, inkos@carrier.kiev.ua Отпечатано с диапозитивов, изготовленных ООО «Гуманитарный издательский центр ВЛАДОС». Типография «Диса Плюс» 04116, г.Киев, а/я 33 Формат 60X90/16. Печать офсетная. Бумага газетная. Усл. печ. л. 27 + 0,5 ил. Тираж 3 000 экз. Заказ № Wo/ Гуманитарный издательский центр ВЛАДОС. 119571, Москва, просп. Вернадского, 88, Московский педагогический государственный университет. Тел. 437-11-11, 437-25-52, 437-99-98; тел./факс 735-66-25. E-mail: vlados@dol.ru http://www.vlados.ru
[1] Oil and water will never mix. 2. Suspicion always haunts the guilty mind. 3. Familiarity breeds contempt. 4. It's not the gay coat that makes the gentleman. [2] The spelling theater is common in the American variant of the English language.
[4] The most notable public schools are Eton |'i:tn], Harrow ['haenu], Winchester ['wintjists], Rugby ['rAgbi], Oundle ['aundl], Uppingham ['Apioam], Charterhouse ['tjaitshaus], These schools are exclusive boarding schools, which train their pupils for leading positions in society.
[7] Do not insert the unnecessary [w] when the diphthong is followed by a vowel as in this word.
Классическая статистика. Функция распределения Максвелла. Барометрическая формула. Распределение Больцмана. Закон равномерного распределения энергии по степеням свободы молекул.
В классической статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/ 2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень «обладает» вдвое большей энергией потому, что на нее приходится не только кинетическая энергия (как в случае поступательного и вращательного движений), но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы. Таким образом, средняя энергия молекулы
где i — сумма числа поступательных, числа вращательных в удвоенного числа колебательных степеней свободы молекулы:
Внутренняя энергия для произвольной массы т газа.
где М — молярная масса, n — количество вещества.
dN – число частиц, попадающих в определенный интервал скоростей. N – число всех частиц. f(V) – функция распределения по скоростям dV – элементарный объем скоростей.
Рассмотрим функцию распределения по скоростям в сферической системе координат:
Величина А (амплитуда вероятности) находится из условия нормировки:
Аналогично находим j(vy) и j(vz):
тогда
Первое закон термодинамики.
Внутренняя энергия системы. Теплоемкость вещества. Первый закон термодинамики. Применение первого закона термодинамики к изопроцессам в идеальном газе. Адиабатический процесс.
Внутренняя энергия газа
Теплоемкость вещества.
|












 - функция распределения Максвелла.
- функция распределения Максвелла.
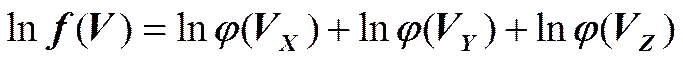








 - условие нормировки
- условие нормировки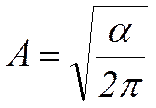 ;
;