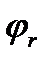Структурный и параметрический синтез регуляторов системы управления технологическим процессом
Системы векторного управления представляют собой класс систем автоматического управления ЭП переменного тока во вращающихся и определённым образом сориентированных системах координат с подчинённым регулированием переменных. Способ ориентации системы координат по вектору потокосцепления ротора управляемого АД делает схожим организацию системы векторного управления на структуру управления классическим ЭП постоянного тока с независимым возбуждением. Согласно анализу требований, предъявляемых к моментному ЭП, для управления АД в составе нагрузочного испытательного стенда наиболее подходящим способом является именно векторное управление с ориентацией системы координат по вектору потокосцепления ротора. В рамках синтеза управляющей системы предполагается разработка модифицированной системы векторного управления с учётом особенностей работы нагрузочного асинхронного ЭП в составе испытательного стенда. При синтезе регуляторов для управления составляющим и вектора тока статора и потокосцеплением ротора использовался метод определения желаемой передаточной функции с настройкой на модульный оптимум. Для контуров управления частотой вращения и положением, ввиду минимизацииошибкиповозмущениюиспользовананастройканасимметричный оптимум. По итогам синтеза регуляторов показатели качества в линеаризованной системе соответствуют ожидаемым значениям. Контуры управления составляющими вектора тока статора Для нахождения требуемой передаточной функции регулятора
Рисунок 12 – Контур управления составляющей пространственного вектора тока статора
Согласно методике настройки на модульный оптимум, получаем выражение для передаточной функции регулятора:
где
– передаточная функция эталонного разомкнутого контура, оптимизированного на модульный оптимум, а В итоге синтезирован пропорционально-интегральный регулятор со следующими параметрами:
– коэффициент усиления,
– постоянная времени интегрирования. Для проверки соответствия показателей качества оптимизированного контура ожидаемым значениям, проведём расчёт переходных процессов
Рисунок 13 – График расчёта переходных процессов в оптимизированном контуре управления составляющей пространственного вектора тока
Рисунок 14 – Контур управления составляющей пространственного вектора тока статора Таким образом, для контура управления составляющей пространственного вектора тока статора
В итоге получаем пропорционально-интегральный регулятор со следующими параметрами:
– коэффициент усиления,
– постоянная времени интегрирования.
Рисунок 15 – График расчёта переходных процессов в оптимизированном контуре управления составляющей пространственного вектора тока
Контур управления потокосцеплением ротора
Рисунок 16 – Контур управления потокосцеплением ротора
В итоге для передаточной функции регулятора получаем следующее выражение:
В итоге синтеза оказался получен пропорционально-интегральный регулятор со следующими параметрами:
– коэффициент усиления и
– постоянная времени интегрирования регулятора потокосцепления.
Рисунок 17 – График расчёта переходных процессов в оптимизированном контуре управления потокосцеплением ротора Контур управления частотой вращения При оптимизации контура управления частотой вращения
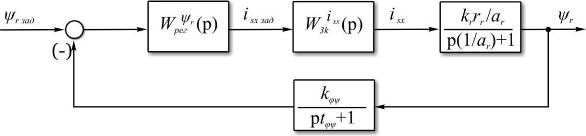
Рисунок 18 – Контур управления частотой вращения Согласно методике настройки на симметричный оптимум, получаем выражение для передаточной функции регулятора скорости
где
– это передаточная функция эталонного разомкнутого контура скорости, оптимизированного на симметричный оптимум, а
– это передаточная функция замкнутого контура управления составляющей вектора тока Тогда итоговое выражение для передаточной функции регулятора в контуре скорости получаем в следующем виде:
Выражение передаточной функции регулятора имеет «неудобный» вид для синтеза регулятора. Предлагается с учётом некоторых допущений, связанных с пренебрежением постоянными времени высших порядков выполнить ряд преобразований над числителем для его представления в более «удобном» виде.
Рисунок 19 – График расчёта переходных процессов в оптимизированном контуре управления частотой вращения ротора
В итоге синтеза оказался получен пропорционально-интегральный регулятор со следующими параметрами:
– коэффициент усиления,
– постоянная времени интегрирования регулятора скорости,
– постоянная времени входного фильтра.
Контур управления положением Согласно иерархии подчинённого регулирования для контура управления частотой вращения внешним является контур управления положением. При оптимизации контура управления положением предполагаем использование настройки на симметричный оптимум.
Рисунок 20 – Контур управления положением
Согласно методике настройки на симметричный оптимум, получаем необходимое выражение для передаточной функции регулятора
где
это передаточная функция эталонного разомкнутого контура положения, оптимизированного на симметричный оптимум, а
это передаточная функция замкнутого контура управления частотой вращения ротора В стремлении понизить порядок передаточной функции объекта управления допустимо не учитывать постоянные времени высших порядков. Применительно к замкнутому контуру скорости
C учётом допущения (3.51) получаем следующее выражение для передаточной функции регулятора в контуре положения:
Для величины малой некомпенсируемой постоянной времени в контуре положения принимаем значение
т.е., что позволяет упростить структуру управляющего регулятора. Итоговое выражение для регулятора положения приобретает следующий вид:
По итогам синтеза оказался получен пропорционально-интегральный регулятор со следующими параметрами:
– коэффициент усиления,
– постоянная времени интегрирования регулятора скорости,
– постоянная времени входного фильтра.
Рисунок 21 – График расчёта переходных процессов в оптимизированном контуре управления положением
|

 (p) выделим из всей системы ЭП отдельно взятый контур, рисунок 18 и сопоставим передаточную функцию объекта управления с желаемой с учётом используемой системы относительных единиц.
(p) выделим из всей системы ЭП отдельно взятый контур, рисунок 18 и сопоставим передаточную функцию объекта управления с желаемой с учётом используемой системы относительных единиц.

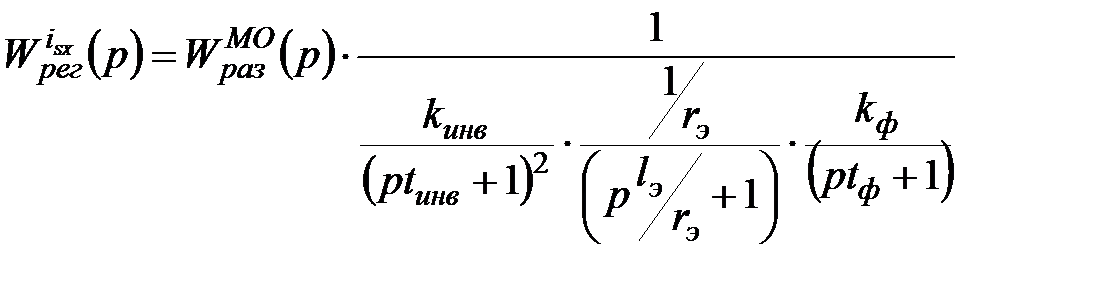 , (2.12)
, (2.12)
 – малая некомпенсируемая постоянная времени, определяющая быстродействие контура после оптимизации.
– малая некомпенсируемая постоянная времени, определяющая быстродействие контура после оптимизации.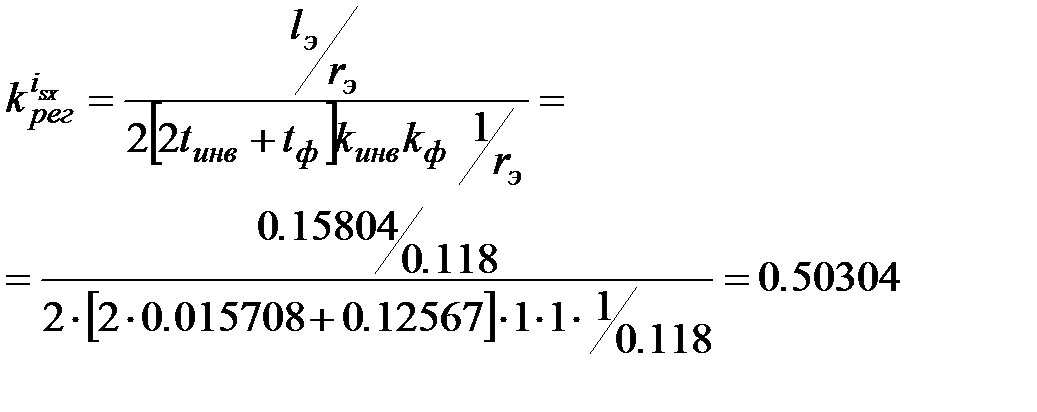 (2.13)
(2.13)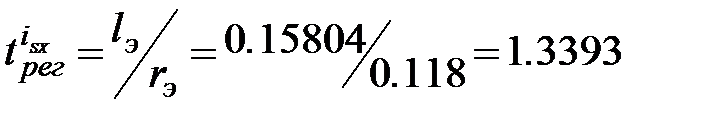

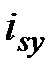
 :
: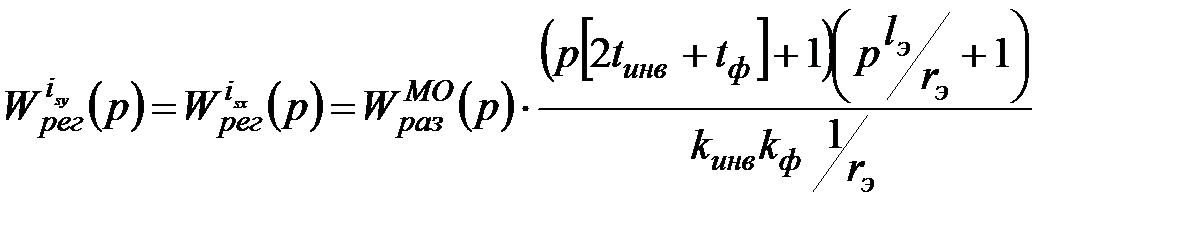 .(2.14)
.(2.14) (2.15)
(2.15)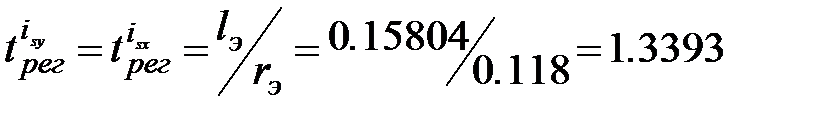

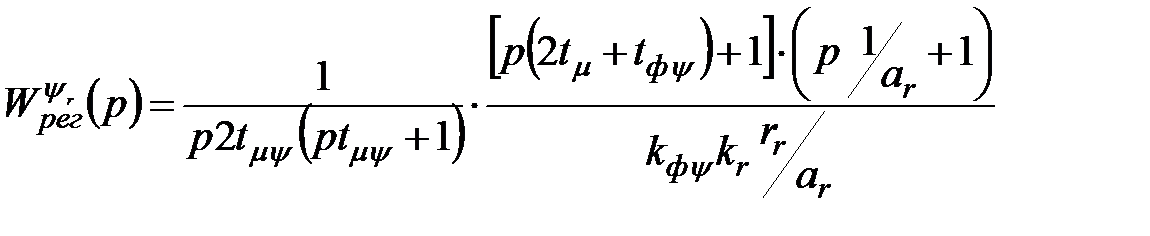 .(2.16)
.(2.16)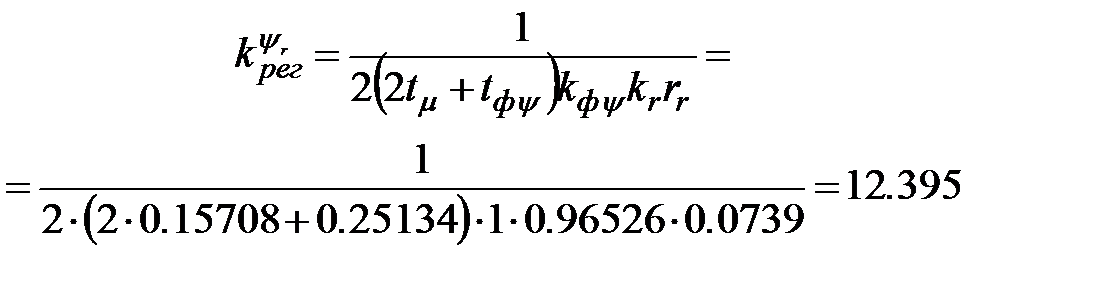 (2.17)
(2.17) (о.е.)(2.18)
(о.е.)(2.18) необходимо использовать настройку на симметричный оптимум, так как в данном случае объект управления содержит интегральное звено, что приводит к необходимости использования пропорционального регулятора при настройке на модульный оптимум и делает невозможным получение системы астатической по возмущению. Именно поэтому при оптимизации контура скорости используем настройку на симметричный оптимум, а для приближения характеристик контура после оптимизации к характеристикам, соответствующим настройке на модульный оптимум на входе контура установим фильтр в виде апериодического звена.
необходимо использовать настройку на симметричный оптимум, так как в данном случае объект управления содержит интегральное звено, что приводит к необходимости использования пропорционального регулятора при настройке на модульный оптимум и делает невозможным получение системы астатической по возмущению. Именно поэтому при оптимизации контура скорости используем настройку на симметричный оптимум, а для приближения характеристик контура после оптимизации к характеристикам, соответствующим настройке на модульный оптимум на входе контура установим фильтр в виде апериодического звена.
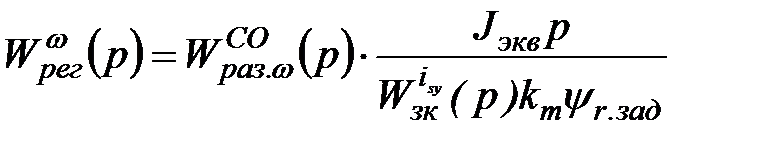 ,(2.19)
,(2.19)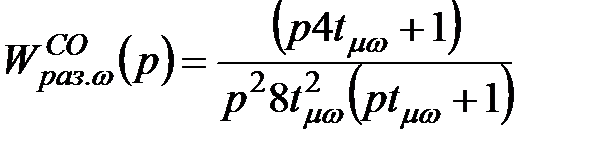
 – малая некомпенсируемая постоянная времени, определяющая быстродействие контура;
– малая некомпенсируемая постоянная времени, определяющая быстродействие контура;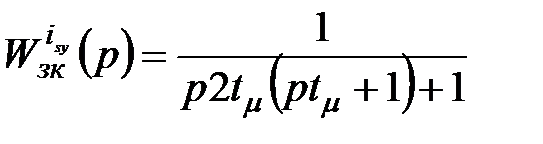 (2.20)
(2.20) , в данном случае являющаяся подчинённым контуром для контура частоты вращения.
, в данном случае являющаяся подчинённым контуром для контура частоты вращения.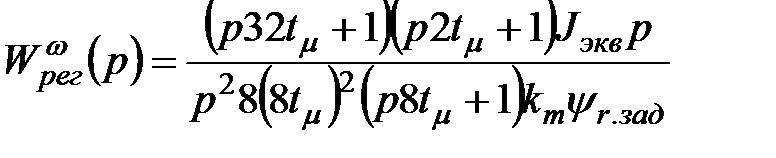 . (2.21)
. (2.21)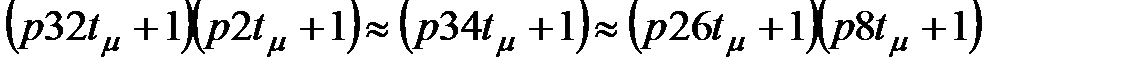 .(2.22)
.(2.22) .
.
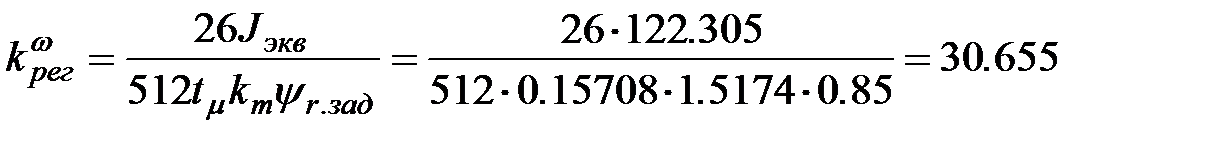 (о.е.)
(о.е.)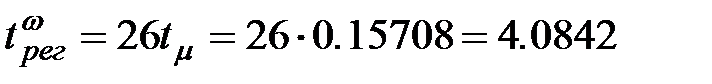 (о.е.)
(о.е.)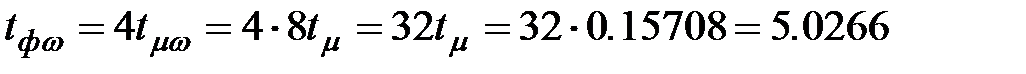 (о.е.)
(о.е.)

 ,(2.23)
,(2.23)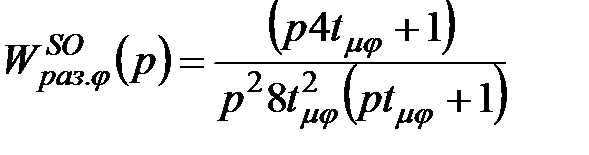
 – малая некомпенсируемая постоянная времени, определяющая быстродействие данного контура;
– малая некомпенсируемая постоянная времени, определяющая быстродействие данного контура;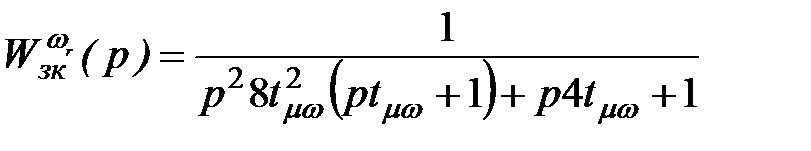 (2.24)
(2.24)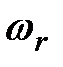 , настроенного на симметричный оптимум с фильтром на входе и являющегося подчинённым относительно контура положения.
, настроенного на симметричный оптимум с фильтром на входе и являющегося подчинённым относительно контура положения. это выглядит следующим образом:
это выглядит следующим образом: . (2.25)
. (2.25)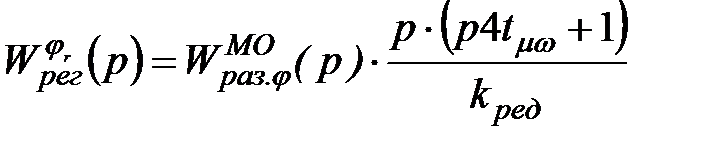 . (2.26)
. (2.26)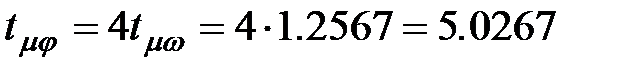 (2.27)
(2.27) . (2.28)
. (2.28) (о.е.)
(о.е.)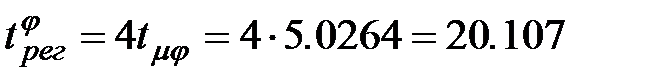 (о.е.)
(о.е.) (о.е.)
(о.е.)