Выбор среды моделирования и разработка математической модели технологического процесса и технологического оборудования с исполнительными электроприводами
Моделирование работы технологического процесса будем проводить в среде MATLAB Simulink, обладающей широкими возможностями выполнения математического моделирования, создавая модель из простых блоков. Также в среде Simulink содержаться блоки, которые позволяют визуализировать процессы моделирования. Математическое описание процессов в асинхронном двигателе Математическое описание АД должно отражать особенности эксплуатационных режимов работы нагрузочного моментного ЭП в составе испытательного стенда. Кроме того, в дальнейшем данная имитационная модель рассматривается как объект оптимального управления, на основании которого выполняется структурно-параметрический синтез системы векторного управления АД. При составлении уравнений электрического равновесия в обмотках АД возьмём за основу систему уравнений для трёхфазной электрической машины и ряд допущений, общепринятых в теории электрических машин переменного тока: параметры обмоток всех фаз имеют одинаковые значения, т.е. имеет место симметричный режим работы; магнитное поле электрической машины имеет синусоидальное распределение вдоль воздушного зазора; принимаем напряжения на выходе ПЧ синусоидальной формы, заведомо не учитывая взаимного влияния между АД и ПЧ по силовому каналу; не учитываются потери в стали, вызываемые протеканием вихревых токов в магнито проводе двигателя и его перемагничением; насыщение магнитной цепи АД не учитывается благодаря наложению ограничений на статорные токи; эффект вытеснения токов в проводниках ротора пренебрежимо мал ввиду того, что частота токов ротора при питании от ПЧ ограничена рабочим участком механической характеристики. На основании второго закона Кирхгофа и с учётом вышеприведённых допущений, уравнения для ЭДС в обмотках статора и ротора АД можно представить в следующем виде:
для цепей статора и
для цепей ротора.
В представленных системах уравнений приняты следующие обозначения:
Для связи между потокосцеплениями и токами в обмотках воспользуемся законом Ампера, тогда:
для статора
для ротора. Уравнения потокосцеплений показывают зависимость от токов в каждой обмотке через взаимоиндукцию. В уравнениях (2.3 и 2.4) коэффициенты Не забывая о том, что системы уравнений (2.1 – 2.4) связывают исключительно скалярные величины, выражение для электромагнитного момента представим в следующем виде [60]:
где На основании второго закона Ньютона представим уравнение для движения и равновесия моментов на валу АД:
где Изначально АД является трёхфазной электрической машиной с неявнополюсным ротором. Анализируя режимы работы АД в составе нагрузочного моментного ЭП и совокупность принятых выше допущений можно предположить правомерность использования для математического описания эквивалентной двухфазной модели. На пути упрощения математического описания АД оказался подходящим метод пространственного вектора, позволяющий существенно упростить и сократить вышеприведённую систему уравнений; метод позволяет связать уравнения (2.1 – 2.6) в единую систему с векторными переменными состояния. Суть метода состоит в том, что мгновенные значения симметричных трёхфазных переменных состояния (напряжение, токи, потокосцепления) можно математически преобразовать так, чтобы они были представлены одним пространственным вектором. Представим систему уравнений с векторными переменными состояния для случая с произвольной ориентацией системы координат [21, 36]:
Здесь
Раскрывая содержание пространственных векторов, получаем следующее:
Система координат с принудительной ориентацией по вектору потокосцепления ротора При решении задач разработки систем управления для АД необходимо рассматривать его имитационную модель с позиций объекта оптимального управления. В теории систем управления асинхронными электроприводами при моделировании АД нашел место уникальный принцип ориентации системы координат по вектору потокосцепления ротора. В данном случае имитационная модель АД приобретает определенное сходство со структурной схемой машины постоянного тока, где возможно раздельное управление магнитным состоянием и моментом на валу двигателя. Математически условие ориентации применительно) выражается следующим образом:
В системе
В системе уравнений переменные с индексами «x» и «y» соответствуют компонентам пространственного вектора в координатной системе с ориентацией по вектору потокосцеплений ротора
Рисунок 10 – Структурная схема имитационной модели АД в системе координат с ориентацией по вектору потокосцепления ротора
Модель АД, представленная на рис. удобна для реализации и расчёта в любом из прикладных программных продуктов, поддерживающих объектно-структурное моделирование систем (Simulink-Matlab, Windora и т.д.). Для исследования и проверки адекватности созданной модели АД удобно выполнить её реализацию в среде Simulink-Matlab. В данной системе симметричные трёхфазные напряжения, представленные в относительных единицах подвергаются преобразованию Кларка и поступают в виде компонентов пространственного вектора напряжений
Здесь
Графически преобразование Парка-Горева иллюстрируется на рис.
Рисунок 11 – График преобразований Парка-Горева для связи между вращающейся и стационарной системой координат
Координатный преобразователь Парка-Горева сориентирован совместно с системой координат разработанной имитационной модели АД. Благодаря этому на входы модели по напряжению
|

 (2.1)
(2.1) (2.2)
(2.2) =
= 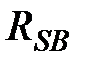 =
=  =
=  – активные сопротивления фаз статора;
– активные сопротивления фаз статора;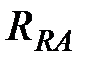 =
=  =
=  =
= 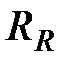 – активные сопротивления фаз ротора;
– активные сопротивления фаз ротора; ,
, 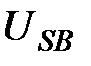 ,
,  ,
,  ,
, 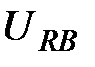 ,
,  – мгновенные фазные напряжения статора и ротора;
– мгновенные фазные напряжения статора и ротора; ,
,  ,
,  ,
,  ,
, 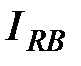 ,
,  – мгновенные фазные токи в обмотках статора и ротора;
– мгновенные фазные токи в обмотках статора и ротора; ,
, 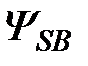 ,
,  ,
,  ,
,  ,
,  – потокосцепления обмоток статора и ротора.
– потокосцепления обмоток статора и ротора. (2.3)
(2.3) (2.4)
(2.4) ,
, 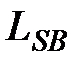 ,
,  ,
,  ,
,  ,
,  являются собственными индуктивностями соответствующих обмоток, все остальные – индуктивности между соответствующими обмотками.
являются собственными индуктивностями соответствующих обмоток, все остальные – индуктивности между соответствующими обмотками. ,(2.5)
,(2.5) это число пар полюсов рассматриваемого АД.
это число пар полюсов рассматриваемого АД. ,(2.6)
,(2.6) – момент инерции на валу АД,
– момент инерции на валу АД,  – угловая частота вращения ротора,
– угловая частота вращения ротора,  – момент развиваемый АД и
– момент развиваемый АД и  – момент приложенный к валу двигателя со стороны нагрузки.
– момент приложенный к валу двигателя со стороны нагрузки. (2.7)
(2.7) ,
,  ,
,  ,
, 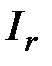 ,
,  и
и  - двухэлементные векторы напряжений, токов и потокосцеплений, представленные в произвольно ориентированной ортогональной (двухфазной) системе координат в виде составляющих по координатным осям. Переменная
- двухэлементные векторы напряжений, токов и потокосцеплений, представленные в произвольно ориентированной ортогональной (двухфазной) системе координат в виде составляющих по координатным осям. Переменная  служит для задания произвольной частоты вращения координатной системы. Вспомогательная матричная константа j служит для «переворота» компонентов векторных переменных и позволяет упростить форму записи системы уравнений.
служит для задания произвольной частоты вращения координатной системы. Вспомогательная матричная константа j служит для «переворота» компонентов векторных переменных и позволяет упростить форму записи системы уравнений. ,
,  ,
,  ,
,  ,
,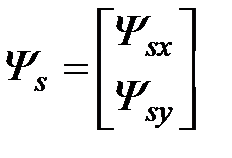 ,
,  ,
,  .(2.8)
.(2.8)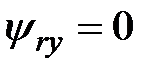 ;
;  ;
; 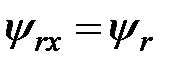 .Уравнения, описывающие АД в системе координат с принудительной ориентацией по вектору потокосцепления ротора.
.Уравнения, описывающие АД в системе координат с принудительной ориентацией по вектору потокосцепления ротора.  (2.9)
(2.9)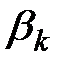 представляет собой скольжение системы координат, а
представляет собой скольжение системы координат, а  соответственно скорость её вращения. Данные параметры определяются в соответствии со следующими выражениями:
соответственно скорость её вращения. Данные параметры определяются в соответствии со следующими выражениями: ;
;  . (2.9)
. (2.9) . С помощью правил создания и преобразования структурных схем, принятых в теории автоматического управления, представим систему уравнений в виде структурной схемы. На рис. представлена структурная схема, имитационной модели АД в системе координат с ориентацией по вектору потокосцепления ротора
. С помощью правил создания и преобразования структурных схем, принятых в теории автоматического управления, представим систему уравнений в виде структурной схемы. На рис. представлена структурная схема, имитационной модели АД в системе координат с ориентацией по вектору потокосцепления ротора  .
.
 и
и  на входы координатного преобразователя Парка-Горева. Формулы для координатного преобразования Парка-Горева, позволяющего реализовать переход от стационарной системы координат к вращающейся представлены ниже:
на входы координатного преобразователя Парка-Горева. Формулы для координатного преобразования Парка-Горева, позволяющего реализовать переход от стационарной системы координат к вращающейся представлены ниже: (2.10)
(2.10)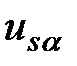 ,
,  - составляющие пространственного вектора напряжения статора
- составляющие пространственного вектора напряжения статора  , представленные в стационарной системе координат;
, представленные в стационарной системе координат; ,
, 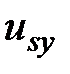 - составляющие вектора напряжения статора
- составляющие вектора напряжения статора  , представленные во вращающейся системе координат;
, представленные во вращающейся системе координат; - угол поворота вращающейся координатной системы (угол ориентации). Параметр
- угол поворота вращающейся координатной системы (угол ориентации). Параметр  связан с угловой скоростью вращения координатной системы
связан с угловой скоростью вращения координатной системы  благодаря следующему выражению:
благодаря следующему выражению: .(2.11)
.(2.11)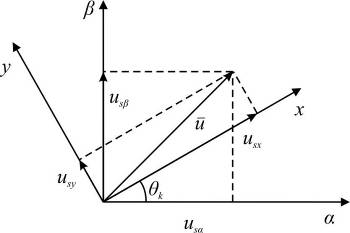
 и
и  поступают компоненты пространственного вектора напряжения, представленного во вращающейся системе координат.
поступают компоненты пространственного вектора напряжения, представленного во вращающейся системе координат.


