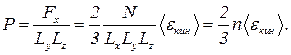Рассмотрим теперь состояние идеального газа с квантовой точки зрения. Пусть частица массы m находится в непроницаемом ящике размером Lx´Ly´Lz. Ее энергия равна  . В отличие от классического описания состояний частицы, квантово-механическое рассмотрение показывает, что проекции импульса могут принимать только дискретный ряд значений:
. В отличие от классического описания состояний частицы, квантово-механическое рассмотрение показывает, что проекции импульса могут принимать только дискретный ряд значений:  ;
;  ;
; 
 здесь
здесь  Этообстоятельство приводит к квантованию энергии частицы. Возможные значения энергии:
Этообстоятельство приводит к квантованию энергии частицы. Возможные значения энергии:
 (22)
(22)
Формула (22) показывает, что энергия любого уровня зависит от размеров ящика. Допустим, одну из стенок ящика (например, перпендикулярную оси OX) заменили поршнем. При уменьшении объема ящика поршнем энергия частицы будет увеличиваться. Значит, чтобы сжать область под поршнем надо совершить работу против силы давления частицы на стенку. Эта сила равна минус производной от энергии по размеру Lx:
 (23)
(23)
Верхний индекс “1” у силы давления означает, что это сила давления одной частицы. В состоянии термодинамического равновесия при тепловом взаимодействии частицы со стенкой и, через нее, с тепловым резервуаром происходит непрерывный переход с уровня на уровень. Давление флуктуирует. Среднее значение силы давления частицы на стенку равно
 (24)
(24)
Далее обратим внимание на то, что в равновесии
 (25)
(25)
Таким образом, в состоянии равновесия сила давления одной частицы на стенку может быть выражена через среднюю энергию
 . (26)
. (26)
Если в ящике N молекул, то сила давления в N раз больше:
 (27)
(27)
Так как площадь стенки равна LyLz, то давление P=Fx/LyLz оказывается точно таким же, как дает классический расчет
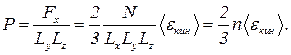

 . В отличие от классического описания состояний частицы, квантово-механическое рассмотрение показывает, что проекции импульса могут принимать только дискретный ряд значений:
. В отличие от классического описания состояний частицы, квантово-механическое рассмотрение показывает, что проекции импульса могут принимать только дискретный ряд значений:  ;
;  ;
; 
 здесь
здесь  Этообстоятельство приводит к квантованию энергии частицы. Возможные значения энергии:
Этообстоятельство приводит к квантованию энергии частицы. Возможные значения энергии:  (22)
(22) (23)
(23) (24)
(24)  (25)
(25)  . (26)
. (26)  (27)
(27)