Во всем дальнейшем курсе мы будем иметь дело либо с равновесными состояниями, либо с процессами, в которых изменения параметров происходят столь медленно, что в каждый момент времени система или ее части можно считать находящимися в состоянии теплового равновесия. Такие процессы называют квазистатическими. Рассмотрим несколько таких процессов.
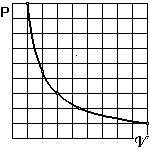 Рис. 16
Рис. 16
|
5.1.1 Изотермический процесс. Если газ находится в емкости переменного объема в хорошем контакте с достаточно большим тепловым резервуаром, поддерживающем постоянной температуру газа, то объем V и давление P изменяются в соответствии с уравнением состояния PV=nRT по закону:
PV=const. (31)
Зависимость P=P(V) графически изображается гиперболой. Эту кривую называют изотермой. В изотермическом процессе к газу либо подводится либо отводится энергия.
 Рис. 17
Рис. 17
|
5.1.2 Изобарический процесс. Изменение состояния газа можно осуществить таким образом, чтобы его давление оставалось постоянным. Можно предложить следующий вариант реализации такого процесса. Заключим газ в вертикально установленный цилиндр, в котором легко подвижным поршнем удерживается газ. На поршень поставим груз некоторой массы.
Если трение поршня о стенки цилиндра пренебрежимо мало то при нагревании или охлаждении газа будет изменяться его объем без изменения давления (которое будет равно весу поршня и груза, деленному на площадь поршня). Это - изобарический процесс. Переменными параметрами в этом процессе являются объем и температура газа. Из уравнения Клапейрона-Менделеева следует, что в данном процессе между ними имеет место прямая пропорциональность. Прямая V(T) выходит из начала координат:
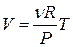 . (32)
. (32)
Тангенс угла наклона прямой V(T) равен 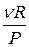 . Как видно, большим давлениям отвечают более пологие прямые.
. Как видно, большим давлениям отвечают более пологие прямые.
5.1.3 Изохорический процесс. Если газ заключен в сосуд неизменного объема, то при нагревании его вместе с температурой будет изменяться давление. Зависимость давления от температуры P(T) описывается в этом случае прямой, выходящей из начала координат. Она называется изохорой. Из уравнения Клапейрона-Меделеева следует, что прямая P(T) описывается уравнением:
 (42)
(42)
Прямая P(T) выходит из начала координат; тангенс угла наклона прямой P(T) равен  . Большим объемам отвечают более пологие прямые.
. Большим объемам отвечают более пологие прямые.

 Процессы, в которых изменяются все три параметра можно изображать кривыми на плоскости двух переменных: (P; T), (V; T) или (P; V). Причем, используя уравнения состояния (применимое для любой точки плоскости переменных), можно переходить от одной пары к другой. Рассмотрим пример такого перехода. Пусть процесс, в котором участвовал разреженный газ описывается прямой на PV -диаграмме (см. рисунок). Прямая описывается уравнением:
Процессы, в которых изменяются все три параметра можно изображать кривыми на плоскости двух переменных: (P; T), (V; T) или (P; V). Причем, используя уравнения состояния (применимое для любой точки плоскости переменных), можно переходить от одной пары к другой. Рассмотрим пример такого перехода. Пусть процесс, в котором участвовал разреженный газ описывается прямой на PV -диаграмме (см. рисунок). Прямая описывается уравнением:
 (43)
(43)
Выясним, как выглядит этот процесс в переменных PT. Для этого с помощью уравнения состояния исключим переменную из правой части уравнения (42). Поскольку 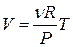 , подстановка этого в (42) дает:
, подстановка этого в (42) дает:
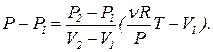 (44)
(44)
Переписывая уравнение (43) по-другому
 , (45)
, (45)
видим, что зависимость T(P) является квадратичной. В новых переменных процесс изображается параболой.

 Рис. 16
Рис. 16
 Рис. 17
Рис. 17
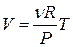 . (32)
. (32) 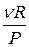 . Как видно, большим давлениям отвечают более пологие прямые.
. Как видно, большим давлениям отвечают более пологие прямые. (42)
(42)  . Большим объемам отвечают более пологие прямые.
. Большим объемам отвечают более пологие прямые.
 Процессы, в которых изменяются все три параметра можно изображать кривыми на плоскости двух переменных: (P; T), (V; T) или (P; V). Причем, используя уравнения состояния (применимое для любой точки плоскости переменных), можно переходить от одной пары к другой. Рассмотрим пример такого перехода. Пусть процесс, в котором участвовал разреженный газ описывается прямой на PV -диаграмме (см. рисунок). Прямая описывается уравнением:
Процессы, в которых изменяются все три параметра можно изображать кривыми на плоскости двух переменных: (P; T), (V; T) или (P; V). Причем, используя уравнения состояния (применимое для любой точки плоскости переменных), можно переходить от одной пары к другой. Рассмотрим пример такого перехода. Пусть процесс, в котором участвовал разреженный газ описывается прямой на PV -диаграмме (см. рисунок). Прямая описывается уравнением:  (43)
(43) 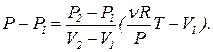 (44)
(44)  , (45)
, (45) 


