Идеальный газ можно рассматривать как собрание свободно двигающихся молекул, между которыми отсутствуют силы взаимного притяжения. Сами молекулы при соударениях между собой и со стенками сосуда ведут себя как абсолютно упругие шарики конечных, но весьма малых размеров.
Реальные газы при не очень низких температурах и не сверхвысоких давлениях близки по своим свойствам и идеальному газу. Давление газа определяется ударами молекул о стенки сосуда. Попробуем вычислить его.
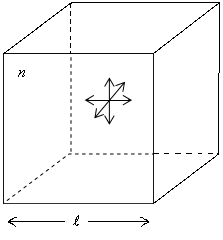 Рис. 2.5 Рис. 2.5
|
Пусть сосуд, в котором находится газ, имеет форму куба со стороной l (рис. 2.5). Внутри куба беспорядочно двигаются n молекул с массой m каждая. Поскольку молекулы двигаются совершенно хаотично, то результат их ударов о стенки будет таков, как если бы 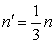 молекул двигались бы прямолинейно между верхней и нижней стенками,
молекул двигались бы прямолинейно между верхней и нижней стенками, 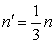 двигалась бы между передней и задней стенками и
двигалась бы между передней и задней стенками и 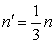 – между левой и правой.
– между левой и правой.
При ударе о стенку молекула упруго отскакивает, и ее импульс mv изменяется на величину
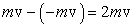 . .
| |
Это изменение импульса определит импульс силы, действующий на молекулу со стороны стенки. Обозначим через Δ F силу удара и через δ t – время удара. Очевидно, что
 . .
| |
По III закону Ньютона сила, численно равная Δ F, будет действовать на стенку. Молекула, отскочив от стенки, долетит до противоположной, отскочит от нее и вернется к первой стенке через время
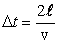 . .
| |
Средняя сила 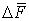 , действующая на стенку за время между двумя последовательными ударами, найдется из условия, что ее импульс
, действующая на стенку за время между двумя последовательными ударами, найдется из условия, что ее импульс 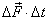 должен быть численно равен импульсу, действующему во время удара, т.е.
должен быть численно равен импульсу, действующему во время удара, т.е.
 . .
| |
Учитывая это, можно записать:
Это среднее значение силы ударов одной молекулы. Но число молекул, движущихся между противоположными стенками, n', и каждая имеет свою скорость. Учтя это, запишем для средней силы 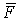 , действующей на стенку:
, действующей на стенку:
 . .
| |
Умножим и поделим полученное выражение на n'. Тогда
 . .
| |
Обозначая
 , ,
| |
назовем полученную величину средней квадратичной скоростью. Учитывая, что 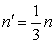 , запишем:
, запишем:
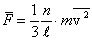 . .
| |
Поделим левую и правую части на l 2, тогда слева будет давление 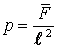 :
:
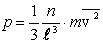 . .
| |
Дробь 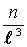 определяет число молекул в единице объема, т.е. концентрацию:
определяет число молекул в единице объема, т.е. концентрацию:
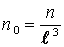 . .
| |
И для давления получаем выражение:
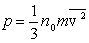 . .
| |
Это и есть основное уравнение молекулярно-кинетической теории газов. Ему можно придать другой вид, умножив и поделив правую часть на 2:
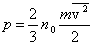 . .
| |
Здесь 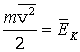 – средняя кинетическая энергия одной молекулы.
– средняя кинетическая энергия одной молекулы.
 . .
| (2.5)
|
Из последней формулы видно, что давление определяется количеством молекул в единице объема и их средней энергией поступательного движения.

 Рис. 2.5
Рис. 2.5
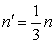 молекул двигались бы прямолинейно между верхней и нижней стенками,
молекул двигались бы прямолинейно между верхней и нижней стенками, 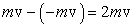 .
.
 .
.
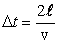 .
.
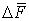 , действующая на стенку за время между двумя последовательными ударами, найдется из условия, что ее импульс
, действующая на стенку за время между двумя последовательными ударами, найдется из условия, что ее импульс 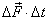 должен быть численно равен импульсу, действующему во время удара, т.е.
должен быть численно равен импульсу, действующему во время удара, т.е. .
.
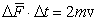 ,
, 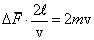 ,
, 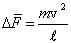 .
.
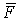 , действующей на стенку:
, действующей на стенку: .
.
 .
.
 ,
,
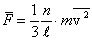 .
.
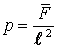 :
: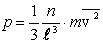 .
.
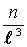 определяет число молекул в единице объема, т.е. концентрацию:
определяет число молекул в единице объема, т.е. концентрацию: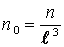 .
.
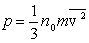 .
.
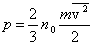 .
.
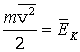 – средняя кинетическая энергия одной молекулы.
– средняя кинетическая энергия одной молекулы. .
.



