Задачи для решения.
Задача № 1. Даны функция спроса Р = 20 – 0,2 · Q и функция предложения Q = 6 · Р – 30, при этом: Q – в тыс. шт., а Р – в грн. Вопросы к задаче № 1: 1. Изобразить графически функции по двум точкам. 2. Определить цены и количество продукции по функции спроса и предложения с шагом изменения цены 5 грн. 3. Определить выручку от реализации продукции по функции спроса и предложения с шагом изменения цены 5 грн. 4. Начертить график функции выручки от реализации продукции по функции спроса и по функции предложения. 5. Сделать вывод, на каком участке функции спроса спрос по цене эластичен и на каком – неэластичный? 6. Максимизирует ли выручку равновесная цена? 7. Дать рекомендации предпринимателю по изменению цены и объёмов продаж.
Пример решения задачи № 1: Данные в задаче функции являются функциями прямой линии. Поэтому, для графического изображения таких функций достаточно задать две любые точки. Например, для функции спроса Р = 20 – 0,2 · Q при Q = 0, Р = 20 грн. (первая точка); при Р = 0 грн., количество продаж Q = 100 тыс. шт. (вторая точка). Для функции предложения Q = 6 · Р – 30 при Р = 0 грн., Q = – 30 тыс. шт. Но – 30 тыс шт. находится вне зоны экономических интересов и означает количество непроданной продукции по Р = 0 грн. Поэтому лучше взять значение Q = 0, тогда Р = 5 грн. Вторую точку можно взять произвольно, например, при Р = 20 грн., Q = 90 тыс. шт. Для графического изображения функций спроса и предложения используют значения максимальной цены и максимального объёма продаж по функции спроса: Р = 20 и Q = 100 тыс. шт., чтобы выбрать удобный масштаб для изображения на плоскости. Тогда график буде иметь следующий вид (рис. 3.1). Чтобы определить цены и количество продаж функции спроса и предложения, необходимо в функции спроса и предложения последовательно подставлять значение цен: 0, 5, 10, 15, 20 грн. и находить значения количества продаж. Расчёты удобно делать в таблице 3.2. Чтобы определить выручку от реализации продукции по функции спроса и предложения используют формулы Поскольку максимальная выручка зависит от расположения функции спроса, то для графического изображения функций выручки обращают внимание на максимальную выручку по функции спроса (рис. 3.2). В нашем примере это – 500 тыс. грн. Тогда на оси ординат достаточно взять 5 делений по 100 тыс. грн. каждое, а по оси абсцис оставить шкалу, принятую для изображения графиков функции спроса и предложения. Таблица 3.2
|

 =
= 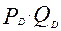 и
и 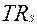 =
=  , также заносят результаты расчётов в табл. 3.1.
, также заносят результаты расчётов в табл. 3.1.


