Значения цены и количества продаж функции спроса и предложения
По изменению выручки от реализации продукции можно определить эластичность участка функции спроса. Если при снижении цены по функции спроса выручка растёт, значит это эластичный участок функции спроса. Если при снижении цены функции спроса выручка уменьшается, значит это неэластичный участок функции спроса. Как видим из графика при снижении цены с 20 до 10 грн. выручка от реализации растёт. Значит это эластичный участок кривой спроса. Дальнейшее снижение цены меньше 10 грн. приводит к росту продаж, но сопровождается снижением выручки от реализации продукции. Поэтому это неэластичный участок кривой спроса, на котором выгодно цены повышать. Равновесную цену по функциям спроса и предложения можно определить по графику или решив систему уравнений. Так по графикам получаем около 12,5 грн., однако это может быть не точная цена. С помощью решения системы уравнений получим следующее значение цены. Как известно, в равновесной точке цена спроса равна цене предложения и величина спроса равна величине предложения. Тогда решим систему двух уравнений:
Р = 20 – 0,2 · Q; Q = 6 · Р – 30 Получим: Р = 20 – 0,2 · (6 · Р – 30) Р = 20 – 0,2 · 6 · Р – 30 · (– 0,2) Р = 20 – 1,2 · Р + 6 Р + 1,2 · Р = 20 + 6 2,2 · Р = 26 Р =
Объём продаж составит: Q = 6 · Р – 30 = 6 · 11,82 – 30 = 70,92 – 30 = 40,92 (тыс. шт.);
или: 11,82 = 20 – 0,2 · Q; 0,2 · Q = 20 – 11,82 0,2 · Q = 8,18 Q = Как видим, на графике равновесный объём вообще меньше 40 тыс. грн., что говорит в пользу арифметического определения значений. Однако, для быстроты принятия решений часто на практике использую графическое моделирование событий, которое дает хоть и приблизительные данные, но с реальным порядком цифр. Поэтому графические методы моделирования полезны для принятия экономических решений. В равновесной точке предприниматель получит выручку от реализации равную:
TR = P · Q = 11,82 · 40,92 = 483, 674 (тис. грн.).
Как видно из предыдущих расчётов, выручка максимизируется и достигает 500 тыс. грн. при цене 10 грн. и количестве продаж 50 тыс. шт. Следовательно, выручка фирмы в равновесной точке не максимизируется. Однако предприниматель не может просто снизить цену с 11,82 грн. до 10 грн. и произвести для продажи 50 тыс. шт. изделия. По функции предложения, которая отражает предельные издержки фирмы на 1 единицу продукции, фирма может предложить по цене 10 грн. только 30 тыс. шт., а не 50 тыс. шт. Чтобы предложить 50 тыс. шт., фирма должна иметь возможность продавать продукцию по 13,3 грн. Продавая 50 тыс. шт. по цене 10 грн., фирма будет получать на каждой штуке убыток 3,3 грн., а на 50 тыс. шт. убыток составит 165 тыс. грн. Поэтому, чтобы максимизировать выручку, фирме нужно сдвинуть функцию предложения вправо на 20 тыс. шт., чтобы она могла по цене 10 грн. производить не 30 тыс. шт., а 50 тыс. шт. Тогда функция предложения будет иметь вид: Q = 6 · Р – 30 + 20 = 6 · Р – 10 (угол наклона сохранился, сдвинулась только линия вправо на 20 тыс. шт. В реальной жизни это возможно, если снизить себестоимость производства 1 единицы продукции и производить 50 тыс. шт. не по 13,33 грн. за шт., а по 10 грн. за шт. Когда Q = 6 · Р – 30, если Q = 50, то Р = Когда Q = 6 · Р – 10, если Q = 50, то Р = Ответ: Чтобы максимизировать выручку, фирме нужно организовать производство 50 тыс. шт. по цене 10 грн., снизив себестоимость производства 1 единицы продукции с 13,33 до 10 грн. за штуку.
Задача № 2. По данным предыдущей задачи определить эластичность спроса и предложения при изменении цены с 5 до 15 грн.
Задача № 3. Дано два комплементарных товара Х и У. Цена на товар У изменилась на 2 %, при этом фирма увеличила количество продаж товара Х с 10 тыс. шт. до 12 тыс. шт. Определить перекрёстную эластичность по цене товара Х при изменении цены на товар У.
Задача № 4. Средние доходы потребителей товара "А" повысились на 5 %. В результате фирма увеличила количество продаж товара "А" с 100 шт. до 115 шт. в неделю. Какова эластичность спроса по доходу на товар "А"?
Задача № 5. Изобразить на графике гипотетические функции спроса и предложения с разными углами наклона относительно оси абсцисс. Снять с графика значения равновесной точки. Взять на функции спроса две произвольные точки, снять сних координаты, добавить к цене 20 % налога на добавленную стоимость и смоделировать ситуацию на рынке по цене и количеству продаж. Как изменится величина спроса и цена? Как распределится налоговое бремя между производителем и потребителем?
Задача № 6. Даны функция спроса Р = 800 – 1,2 · Q и функция предложения Q = 150 + 0,25 · Р, при этом: Q – в шт., а Р – в грн. Вопросы к задаче № 6: 8. Изобразить графически функции по двум точкам. 9. Определить цены и количество продукции по функции спроса и предложения с шагом изменения цены 100 грн. 10. Определить выручку от реализации продукции по функции спроса и предложения с шагом изменения цены 100 грн. 11. Начертить график функции выручки от реализации продукции по функции спроса и по функции предложения. 12. Сделать вывод, на каком участке функции спроса спрос по цене эластичен и на каком – неэластичный? 13. Максимизирует ли выручку равновесная цена? 14. Дать рекомендации предпринимателю по изменению цены и объёмов продаж.
Домашнее задание: 1. Решить задачи № 5 и № 6. 2. На следующее практическое занятие решить задание курсового проектирования № 1 – 6.
|

 , тыс. шт.
, тыс. шт.
 , тыс. шт.
, тыс. шт.
 , тыс. шт.
, тыс. шт.
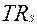 , тыс. шт.
, тыс. шт.
 = 11,82 (грн.) 11 грн. 82 коп., а не 12 грн., как казалось по графику.
= 11,82 (грн.) 11 грн. 82 коп., а не 12 грн., как казалось по графику.
 = 40,9 (тыс. шт.).
= 40,9 (тыс. шт.).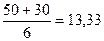 (грн.).
(грн.). (грн.)
(грн.)


